二分虽然思想简单，做了两天的题下来发现实际应用到题目中并没有想象中那么轻松,在此记录下笔记和归纳总结一下几道题目的ac过程以备以后复习时使用。



二分的思想很简单，以下给出定义。

给定一个升序排列的数组 nums ，在其中寻找某个值target，设两个指针 l r 分别指向> 数组左右边界，每次取区间的中点 l+r>>1 为 mid ，当 nums[mid]>targer 的时候说明元素在 [l, mid-1] 之间，反之则在 [mid+1,r] ，当两种情况都不满足，则 nums[mid] 必定为要寻找的 target

如果光知道定义是不足以应用到题目之中的，在连续做了几天的二分题看了一堆题解后，我发觉要二分的不是某个值，而是满足某个性质的区间的边界，当数组可以依照某种性质一分为二，即一边 满足性质 ，另一边 不满足性质 ，我们就有可能把满足或不满足性质的边界给二分出来，而往往这个边界就是需要返回的答案。这么说多少有点抽象，下面是给出的示例

如leetcode上这道模板题

ef1.jpg


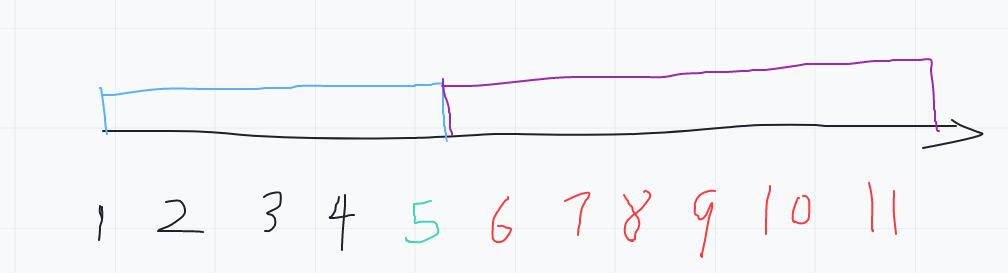
ef2.jpg

如这题，我们将数组一分为二，蓝色是满足性质( <=target 的区间)，紫色是不满足性质(>target)的区间


我们需要做的就是寻找这个蓝色区间的右边界，每次二分一个中值 nums[mid] ，
当 nums[mid]<=target 的时候，我们的边界必定在 [mid,r] 之间(注意mid是有可能取到答案的),nums[mid]>target 的时候，边界必定在 [l,mid-1] 这个区间，每次都缩小范围。

当使用边界的思想，面对一些无单调性但要求在**logn**时间复杂度内做出的题目时，也不至于手足无措，至少可以尝试寻找是否有一个性质能将区间一分为多(菜鸡落泪)进而寻找到边界

实现代码如下

1
2
3
4
5
6
7
8
9
10
int search(int* nums, int numsSize, int target){
    int l=0,r=numsSize-1;
    while(l<r){
        int mid = l + r + 1 >> 1;
        if(nums[mid]<=target) l = mid;
         else r = mid - 1;
    }
    if(nums[l]!=target) return -1;
    return l;
}

疑惑的一点是取中值的时候为什么是 l+r+1>>1 而不是 l+r>>1 ，这是因为在c中除法是向下取整的，这
样会导致当查找区间为 [r-1,r] 的时候，如果是l+r/2，那么区间会更新为**_[l,r]_，下次查找还是 [l,r] 导致死循环，当mid**落在右区间时，即我们需要寻找的是蓝色区域的边界（满足性质）需要补上+1

记一下千锤百炼的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

由以上总结出

具有单调性的题一定可以二分，不具有单调性但可以将区间一分为二的题有可能可以二分


在将做二分题的步骤抽象了之后，尝试做了一道题加深印象

leetcode34 数的范围

题目要求:

ef3.jpg

按上面的思路将题目翻译一下，我们要寻找的是 第一个和最后一个 >=targert 的数，即求上下界的索引位置

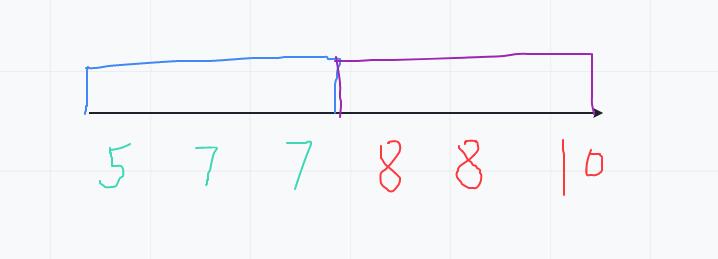
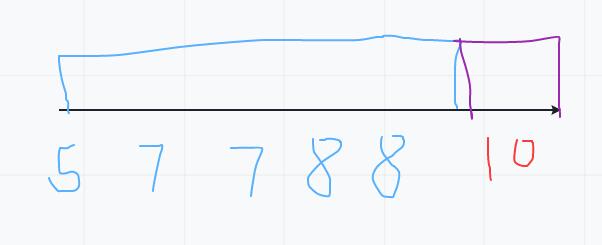
以 [5,7,7,8,8,10] 为例,首先我们需要寻找一个性质，能将数组一分为二，不难发现我们可以分为以下两个区间

ef4.jpg

即 <target 的数分为蓝色区间， >=target 的数分为紫色区间


可以看到，我们要取的元素是紫色区间的左边界。设 mid 为数组的中值，之后判断是否满足 nums[mid]>=target，

如果是的话，那么要查找的元素肯定在 [l,mid] 之间(_因为nums[mid]如果大于target，后面的元素就不可能是target，如果nums[mid]==target，也有可能是最后一个target，我们需要在前半段继续查找)_，当 l=r 时区间里只有一个元素，也就找到了第一个target


这里的二分这么写 
1
2
3
4
5
6
7
8
9
10
11
.....
int l=0,r=numsSize-1;
//我们需要判断一下数组是否为空，为空的话直接返回[-1,-1](在前面略过代码处已定义)
if(r==-1)
    return ret;
while(l<r){
    int mid = l+r>>1;
    if(nums[mid]>=target)
        r = mid;
    else l = mid+1;
}

接下来的查找最后一个 >=target 的元素就并不那么容易了，同样我们依照上面的性质将区间一分为二

ef5.jpg

蓝色区间满足 <=target 紫色区间满足 >target

我们需要查找的元素，实际上是蓝色区间的 右边界 ，现在我们要把它二分出来

同样取中值 mid，判断 nums[mid]>target 是否成立，如果成立的话，答案一定在 [l,mid-1] 这个区间里，如果不成立（即小于等于target），我们将区间缩小为 [mid,r] (_分两种情况讨论，如果nums[mid]==target的话，不一定是最后一个元素，我们需要继续往右边查找，将区间设置为 [mid,r]_)

1
2
3
4
5
6
7
8
9
while(l<r){
   //上面已经记过为什么要+1了
	int mid = l+r+1>>1;
	if(nums[mid]>target){
		r = mid;
	}else{
		l = mid;
	}
}

完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int* searchRange(int* nums, int numsSize, int target,int* returnSize){
    *returnSize = 2;
	int * ret = (int *)malloc(sizeof(int) * 2);
    ret[0] = -1;
    ret[1] = -1;

    int l=0,r=numsSize-1;
    if(r==-1)
        return ret;
    while(l<r){
        int mid = l+r>>1;
        if(nums[mid]>=target)
            r = mid;
        else l = mid+1;
    }
    if(nums[l]==target) ret[0] = l;
    l=0,r=numsSize-1;
    while(l<r){
        int mid = l+r+1>>1;
        if(nums[mid]>target) r = mid-1;
        else l=mid;
    }
    if(nums[l]==target) ret[1] = r;
    return ret;
}

ef6.jpg