二维前缀和与差分笔记
前缀和
什么是前缀和?
给出数组 a[] (a[1],a[2],….a[n])
设数组 b[] 为数组 a[] 的前缀和数组,即
b[i] = a[1] + a[2] + a[3] + …. + a[i]
前缀和的下标一定要从1开始,避免无必要的对下标进行转换
前缀和的作用主要是用于快速筛选出一段区间的和。如对于 a[] 数组想要得出 [l,r] 区间内的和,最容易想到的便是暴力遍历的方式。但对于多次询问,我们可以牺牲一点空间构造出前缀和数组 sum[] ,之后对于每次询问我们都可以用 O(1) 的时间复杂度很方便的得出答案
一维前缀和
具体处理:
做一个预处理,定义一个 sum[] 数组,sum[i] 代表 a 数组中前 i 项的和
1 | const int N=1e5+10; |
查询操作:
对于每次查询,只需返回 sum[r]-sum[l-1] ,时间复杂度为 O(1)
1 | scanf("%d%d",&l,&r); |
二维前缀和
我们可以用前缀和的思想来做这道题,首先构建一个新的二维数组(矩阵) sum[][] 来存储前缀和
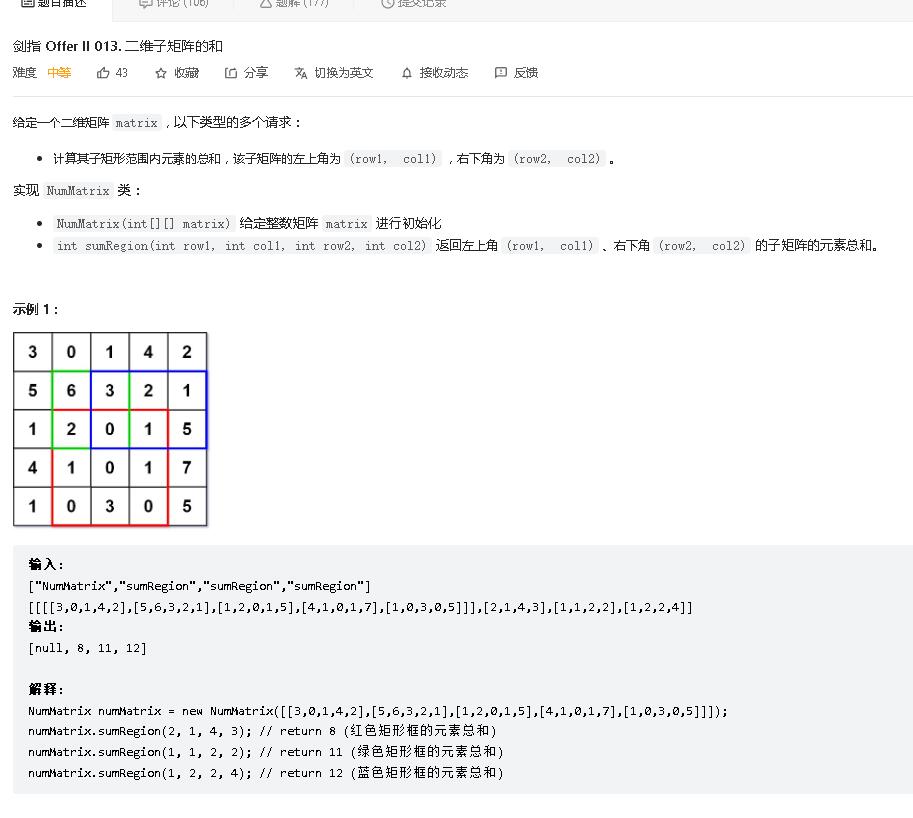
我们需要做一个预处理让 sum[i][j] 为 (i,j) 左上角所有下标元素的和。
结合图片得出二维前缀和预处理公式
sum[i][j] = sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+a[i][j]
(sum[i][j-1]+sum[i-1][j]时sum[i-1][j-1]被加了两次,需要减掉一次)
代码这么写
1 | for (int i = 1; i <= n; i++) |
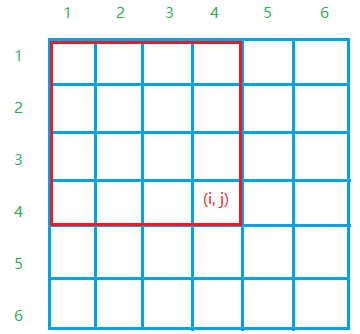
回到题目上,给出子矩阵左上角 (x1,y1) 及右下角 (x2,y2) ,求该矩阵内所有元素的和。
有了前面前缀和后的处理,我们只需要把面积推导一下就好了,这个过程的时间复杂度依然是 O(1) ,是不是比遍历一遍快多了?
得出(x1,y1),(x2,y2)子矩阵的和为:
sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]
该题完整代码如下:
1 | #include<iostream> |
之前做过一道标签是二分前缀和的题目:
leetcode209 长度最小的子数组使用二分查找求解
差分
给定一个原定数组 a[] , 构造一个 b[] 数组,使得
a[i] = b[1]+b[2]+…..+b[i]
也就是说 a[] 是 b[] 的前缀和数组,反过来 b[] 是 a[] 的差分数组
我们考虑怎么构建差分数组 b[] ,如下
b[1] = a[1]-a[0],
b[2] = a[2]-a[1],
……..
b[n] = a[n]-a[n-1]
我们只要有了 b[] 数组,就可以通过前缀和运算 在 O(1) 的时间复杂度内得到原数组 a[] ,由此我们可以将差分理解为前缀和的逆运算
那么差分有什么用呢? 让我们看这么一个问题
给定区间 [l,r] ,让我们为数组 a[] 中的这段区间每个元素都加上c
最容易想到暴力的做法,我们遍历一遍该区间,分别为每个元素加上c。如果我们要进行m次操作,那么时间复杂度就是 O(N*M) 。有更高效的做法吗?我们可以使用差分来操作
设 b[] 为 a[] 的差分数组,考虑通过 b[] 来求得 a[] 数组,任一个 b[i] 的改变会影响 a[i] 及之后的元素求值,所以我们只需进行以下两步操作即可完成对某段区间+c
b[l]+=c,b[r+1]-=c
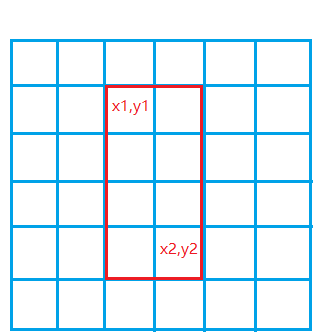
画一个图来解释该公式
b[l]+=c 使得 a[] 中 l及后面的元素都加上 c (红色部分)。但我们所要求的只是[l,r]之间加上c,于是还需要打一个补丁,让 b[r+1]-=c 即 r后面的部分减去前面加的c (绿色部分),这样r后面的区间不会有任何变化
本文标题:二维前缀和与差分笔记
文章作者:meteor
发布时间:2022-06-14
最后更新:2022-06-14
版权声明:本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 CN 许可协议。转载请注明出处!
分享