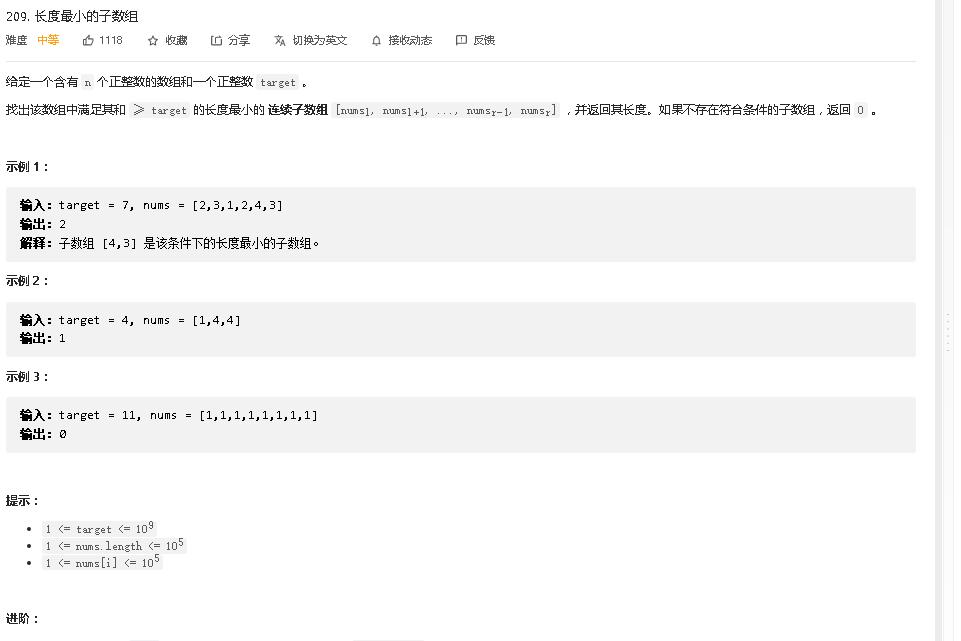
leetcode209长度最小的子数组使用二分查找求解
题解:
题目标签是二分查找,但给出数组是无序的,使用二分查找的方法需新建一个
sum[numberSize] 数组,sum[i] 存储 nums[0]- nums[i] 的和
因为题目给出的是正整数,这样可以确认sum 数组是单调递增的。我们只需要找到 sum[k]-sum[j]>=target ,那么k-j 便是和大于等于target且连续的子数组,当然不一定是最小的,我们需要一直查找比较。
再使用一层for循环来遍历k吗?这样效率不会比暴力算高很多,前面提过sum[] 数组是单调递增的,我们只需要将等式两边变换一下,改为 sum[k] >= sum[j]+target,这样我们每次都将target和前k项和相加作为参数传入二分查找,来取得 k (sum[j]+target的上界)。
1 | //取得target的上界 |
本文标题:leetcode209长度最小的子数组使用二分查找求解
文章作者:meteor
发布时间:2022-09-25
最后更新:2022-09-25
版权声明:本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 CN 许可协议。转载请注明出处!
分享