归并排序模板

归并和 快排 同样属于分治算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int tmp[N];

void merge_sort(int * p,int l,int r){
    //递归的终止条件
    if(l>=r) return;
    //1.确定子问题分界点
    int mid = l+r>>1,i=l,j=mid+1,k=0;
    //2.递归处理子问题
    merge_sort(p,l,mid);
    merge_sort(p,mid+1,r);
    //3.子问题合并
    while(i<=mid&&j<=r){
        if(p[i]<=p[j]) tmp[k++] = p[i++];
        else tmp[k++] = p[j++];
    }
    while(i<=mid) tmp[k++] = p[i++];
    while(j<=r) tmp[k++] = p[j++];
    for(int i=l,j=0;i<=r;i++) p[i] = tmp[j++];
}

在合并子问题时,[l…mid] [mid+1…r] 分别都是有序区间。
为什么递归处理之后会是有序的呢，来模拟一下以下这个序列

1 4 3 6 8 7 5

进入函数时,mid取到 63,于是递归的两个区间被分为

[0…3] [4…6]

进入第一个区间的递归,过程如图

ht.png

右边的 [4…6]区间也是这样处理，回到 mid为 63这里，当两轮递归结束，左右区间已经是有序的了。
此时再执行与子区间相同的归并操作，当整个区间处理完(l>=r时)，问题也就解决了。

排序的时间复杂度分析:

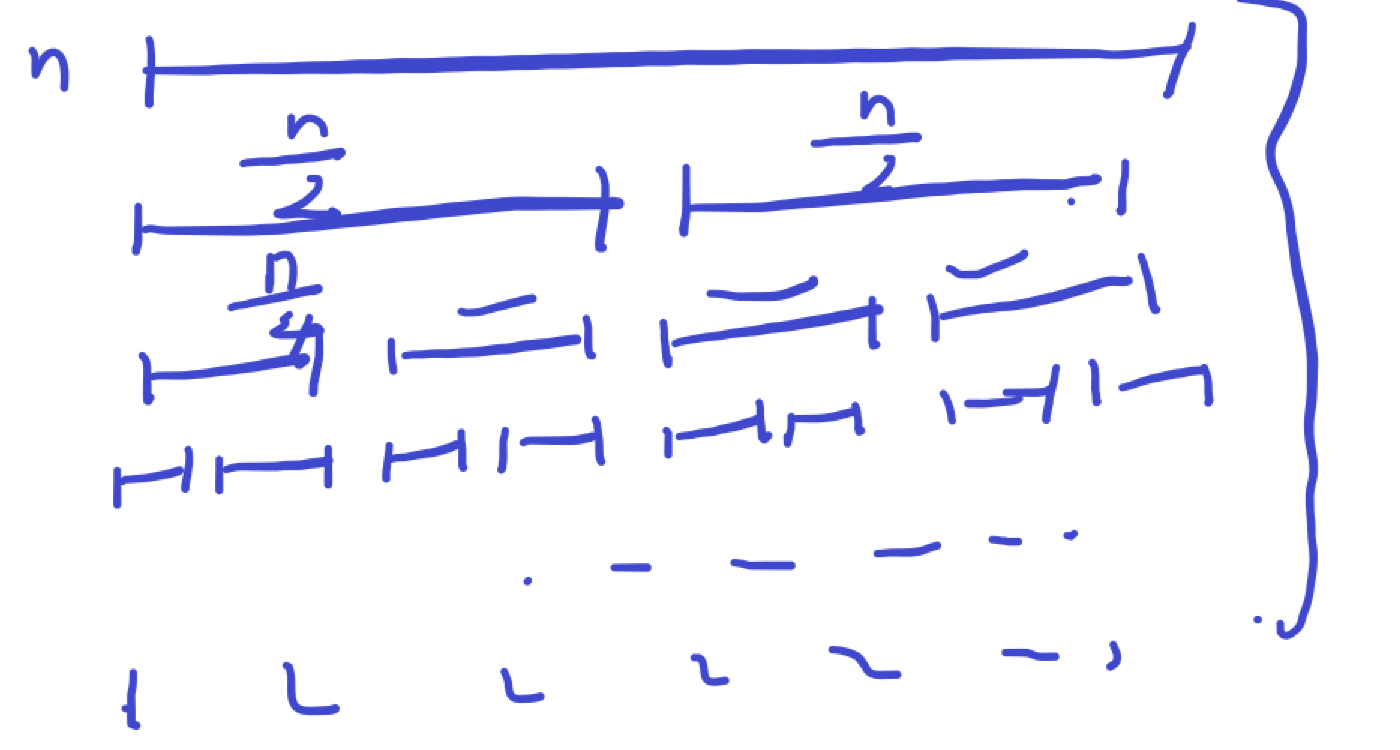
每层递归我们会将序列一分为二，即第一层分为2段 n/2 第三层分为4段 n/4 的区间 ….
每层我们的元素都至少会被扫描一次，即每层递归的时间复杂度都为On
ht2.png

n除以2要除多少次会得到1呢，答案自然是log2n,每层都是On的时间.所以归并排序的时间复杂度为 nlogn
与快排的区别是快排在数据较烂，最坏的情况下会达到 n^2^ 的时间复杂度，而归并排序是稳定的算法，时间复杂度永远都是nlogn