QQ截图20221004001300.png
我们先考虑暴力做法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;

const int N = 1e6+10;
int arry[N];

int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin >> arry[i];
    
    cout << "-1 ";
    for(int i=1;i<n;i++){
        int j=i;
        do j--;while(arry[j]>=arry[i]);
        if(j<0) cout << "-1 ";
        else cout << arry[j] << " ";
    }
    
    return 0;
}

指针i从左到右遍历元素,指针j从i-1的位置开始往左扫描，遇到最近一个<i的元素便输出;

结果当然是愉快的超时咯
QQ截图20221004003536.png

单调栈的考虑思路类似双指针
假设从左到右扫描，每处理一个元素an时，在它入栈前，栈stk[]中维护的是 [a1…an-1]
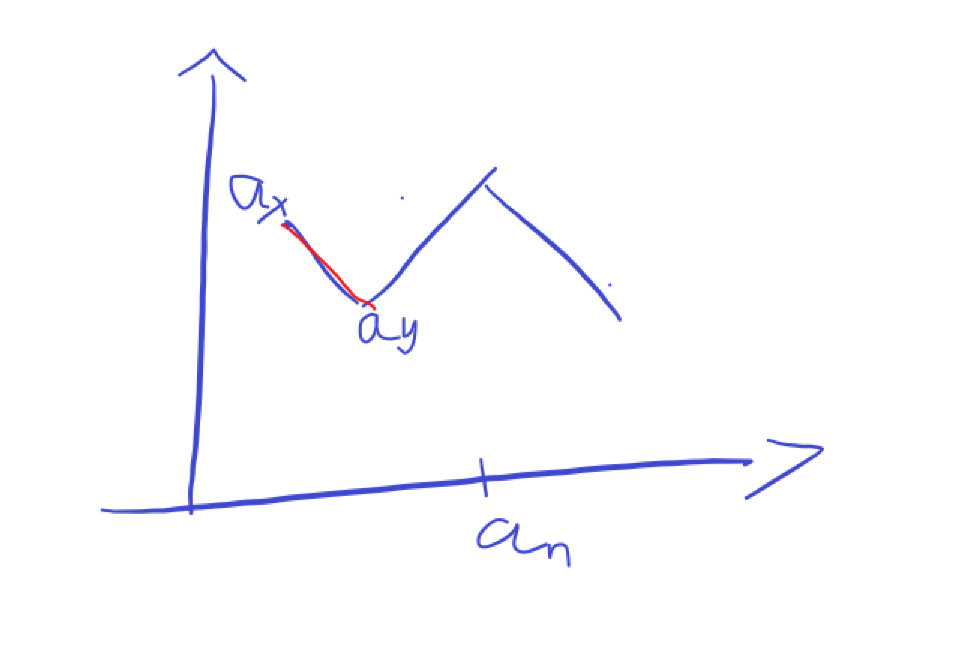
我们可以发现，当stk中拥有元素ax ay且满足

ax>ay; x<y

这样的话，不论后续的元素是什么，ay都会是更优的选择，题目要求的是 “靠右且更小的元素”
QQ截图20221004004646.png
如图，将满足条件的红色逆序对全部删除后，我们可以得到一个单调上升的区间
对于随后每次扫描的an,从栈顶开始遍历，当栈顶的值>=an，便满足了上文所说的性质，an比att更小且更靠右
此时栈顶弹出，即代码中的这一段

1
while(tt&&stk[tt]>=x) tt--;

这一步进行完，如果栈中还有元素，那必定是满足性质的值

1
2
3
       if(tt) cout << stk[tt] << " ";
       else cout << "-1 ";
//否则输出-1

做完别忘了把新的值压入栈

1
stk[++tt] = x;

完整的ac代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;

const int N = 1e6+10;

int stk[N],tt;

int main(){
    int n;
    cin>>n;
    
    cout << tt << endl;

    for(int i=0;i<n;i++){
        int x;
        cin >> x;
        while(tt&&stk[tt]>=x) tt--;
        if(tt) cout << stk[tt] << " ";
        else cout << "-1 ";
        stk[++tt] = x;
    }
    return 0;
}

以及从社区偷的一张dalao画的流程图
lc