NOI2001 食物链（带权并查集）

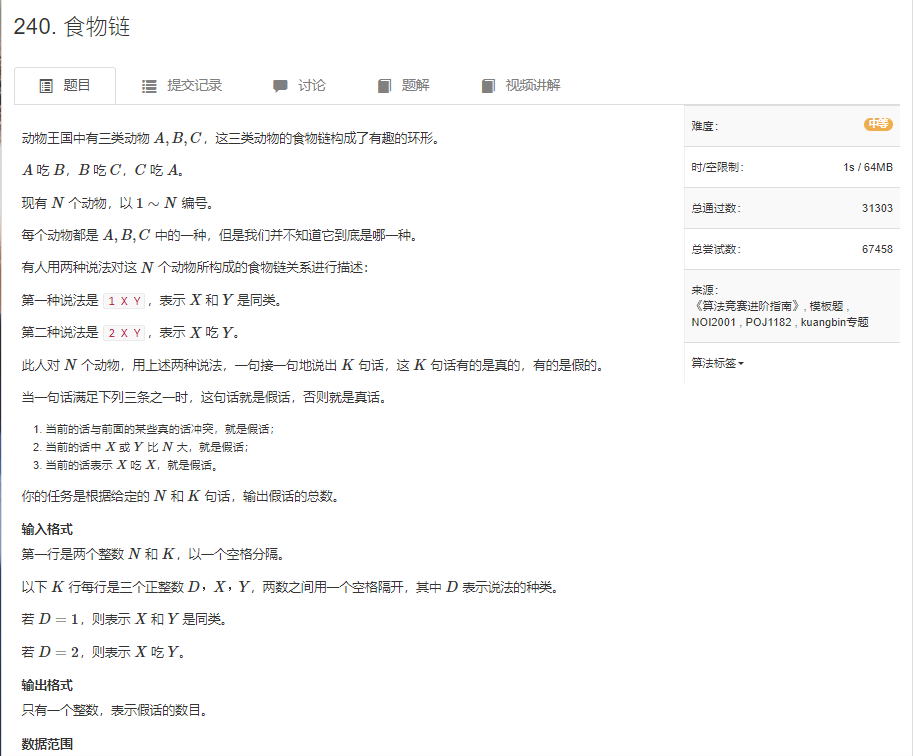
先整理一下思路:
A吃B,B吃C,C吃A，由此形成以下的环形关系

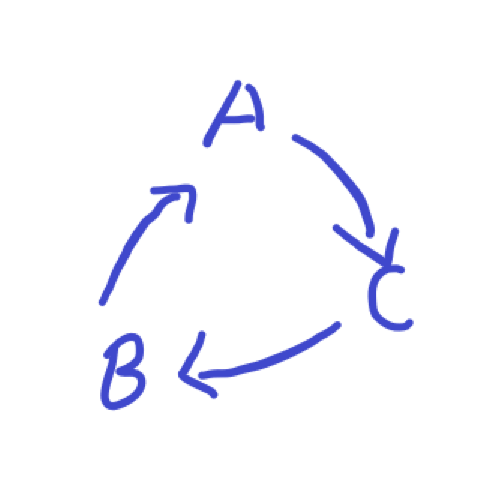
因为会一直循环（即对3取余做条件），我们可以用一个并查集来维护查询他们的身份

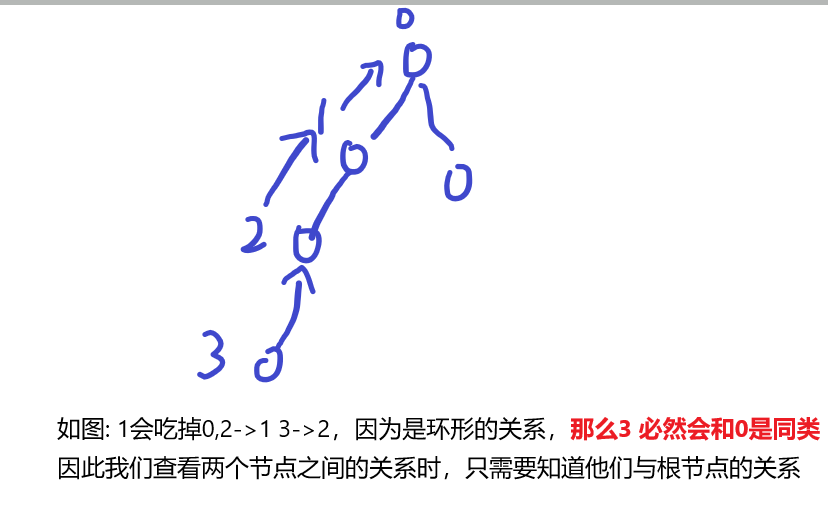
想象一个食人族家庭来说明他们之间的关系
第1代吃掉第0代，第2代吃掉第1代，第3代吃第2代，第0代会吃掉第3代
那么如果有吃掉第3代的第4代，那么他必定与第0代是同一代

采用并查集，维护多一个数组d来表示当前节点到根节点的距离，初始化为0（自身到自身的距离为0）
这个距离对3取模后只能有三种情况

0 1 2

路径压缩:
假设当前并查集状态如下：

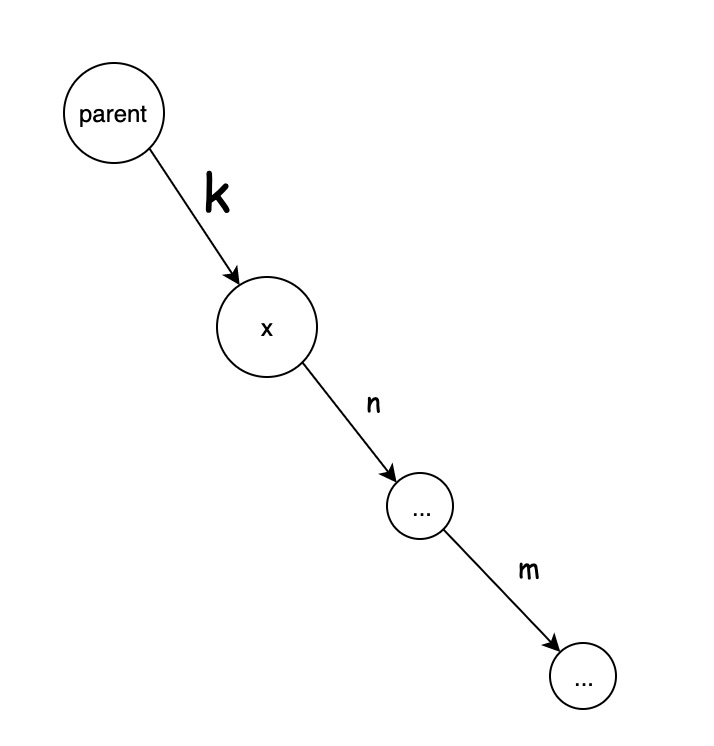
压缩后:

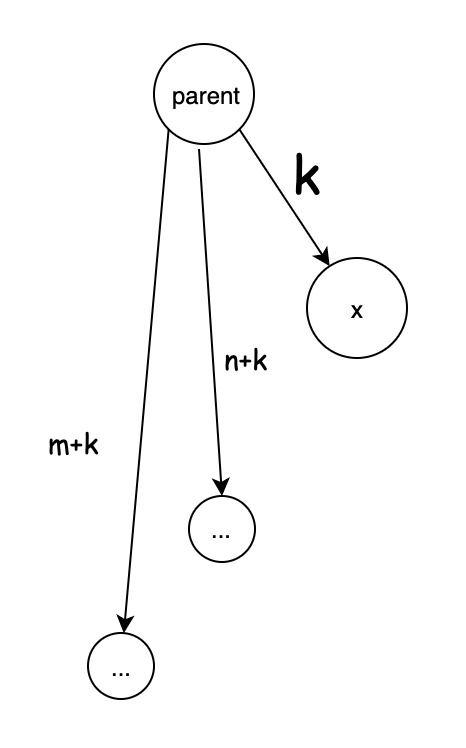
路径压缩的代码:

   if (p[x] != x)
   {
//寻找p[x]的根节点 (会更新d[])
       int t = find(p[x]);
//x到p[x]的距离加上p[x]到根节点root的距离 = x到root的距离
       d[x] += d[p[x]];
//将p[x]指向根节点root
       p[x] = t;
   }

询问类型 1 x和y是同类:
首先判断 x 和 y是否 “在一颗树上”

//如果在x和y的父节点root相同的话，说明已经在先前的询问中处理过关系距离了
//那么判断 d[x]%3==d[y]%3 是否成立，如果不成立的话，谎言次数+1
if(o==1){
    int px = find(x),py= find(y);
    if(px==py&&((d[x]%3)!=(d[y]%3))) res++;
    else {
     //如果根节点不相同的话，进行合并
     p[px] = py;
     d[px] = d[y]-d[x];
    //合并的时候需要计算从 px接到py 这条边的长度
    // d[px]+d[x] = d[y] -> d[px] = d[y]-d[x]
    }
}

询问类型 2 x可以吃掉y
根据以上的分析,x既然可以吃掉y，x与根节点的距离必定比y与根节点的距离大1（对3取模之后)

// (d[x]%3-d[y]%3)=1 -> (d[x]-d[y]-1)%3==0 （条件满足时为谎言)
if(px==py&& (d[x]-d[y]-1)%3) res++;
// 否则执行合并操作
else if(px!=py){
     p[px] = py;
     d[px] = d[y] + 1 - d[x];
}

完整代码如下

#include <iostream>
using namespace std;
const int N = 50000+10;
int p[N],d[N];


//查询父节点
int find(int x){
    if(p[x]!=x){
        int t = find(p[x]);
        d[x]+=d[p[x]];
        p[x] = t;
    }
    return p[x];
}



int main(){
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++) p[i] = i;
    //(((d[x]%3)-(d[y]%3))!=1)
    int res = 0;
    while(k--){
        int o,x,y;
        cin>>o>>x>>y;
        if(x>n||y>n) res++;
        else{
            int px = find(x),py= find(y);
            if(o==1){
                if(px==py&&(d[x] - d[y]) % 3) res++;
                else if(px!=py){
                    p[px] = py;
                    d[px] = d[y]-d[x];
                }
            }else{
                if(px==py&& (d[x]-d[y]-1)%3) res++;
                else if(px!=py){
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }
    
    cout << res;
    
    
    return 0;
}