算法中一些关于质数的概念以及模板整理
首先质数的概念为:
质数(Prime number,又称素数),[1] 指在大于1的自然数中,除了1和该数自身外,无法被其他自然数整除的数
1. 怎么高效判断数n是否为质数?
最为暴力的方法便是从2~n-1中逐个遍历得i,判断n%i==0是否成立,如果成立说明n不为质数(如下代码)
1 | bool is_prime(int x){ |
该代码时间复杂度为O(n),我们可以将他优化一下,将遍历区间从 $[2,n-1]$ 优化到 $[2,√n]$,这是一个质的飞跃!
为什么可以这样做呢?我们想象一下在区间[2,n-1]之间遍历,约数是成对出现的,假如取到i可以整除n 即 $n%i==0$
那么 也会满足 $n%(n%i)==0$,由此看来我们只需枚举约数对中较小的那个即可,即循环继续条件改为 $i<=n/i$,
我们整理一下,有
(举个例子,例如n为12,i为4,12可以被4整除,也可以被12/4(3)整除。)
$$i<=n/i i^{2}^<=n,i<=√n$$
问题得证,我们将背下以下这个模板
1 | bool is_prime(int x) |
2.分解质因数
先补充一下质因数的概念
每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,把一个合数用质因数相乘的形式表示出来,叫做分解质因数。如30=2×3×5 。分解质因数只针对合数。
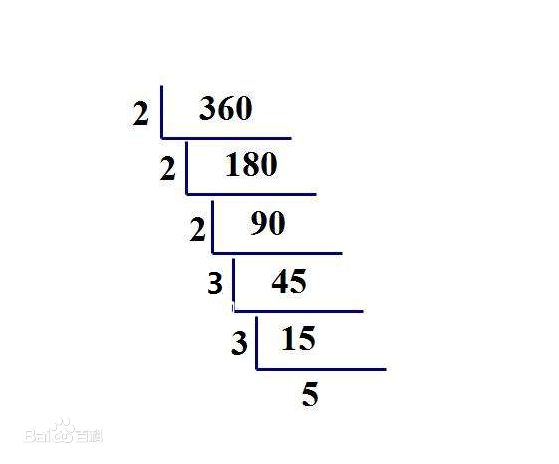
再回忆一下初中的数学知识,我们是怎么手动分解出质因数的
先从定义出发使用最暴力的方法来求出所有质因数,代码如下
1 | void divide(int x) |
同样的,我们也可以像判断质数那样,把时间复杂度优化到O(√n)
1 | void divide(int x) |
为什么可以这么做呢?原因是n中只会包含一个大于√n的质因子,这也是很好证明的
因为 √n x √n = n,如果有2个以上的质因子大于√n,那么结果就矛盾了。
当然,最后需要特判一下x是否大于1,如果大于1,那么x便是唯一的大于根号n的质因子
埃氏筛法:
当需要求2~n中所有质数时,使用埃氏筛法
1 |
|
本文标题:算法中一些关于质数的概念以及模板整理
文章作者:meteor
发布时间:2022-10-14
最后更新:2022-10-14
版权声明:本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 CN 许可协议。转载请注明出处!
分享