计科导论笔记——(2)数字系统

数字系统定义了如何用独特的符号来表示一个数字。在不同的系统中，一个数字有不同的表示方法。例如，两个数字 （2A）16
和 （52）8 都是指同样的数量 （42）10 ,但是它们的表示截然不同。
正如我们再语言中使用符号（字符）来创建单词一样，我们使用符号（数码）来表示数字。但是，我们知道任何语言中的符号数量都是有限的。我们需要重复并组合它们来创建单词。数字也是一样：我们使用有限的数字符号（数码）来表示数字，这意味着数码需要重复使用。
一些数字系统以及在过去广为使用，并可以分为两类: 位置化系统和非位置化系统，着重讨论前者

---

位置化数字系统

在位置化数字系统中，数字中符号所占据的位置决定了表示的值。在该系统，数字这样表示:

+-(Sk-1……..S1S1S0.S-2…S-L)b

它的值是:

n = +-Sk-1*b^k-1^+…+S1*b^1^+S0*b^0^+S-1*b^-1^+S-2*b^-2^+….S-L*b^-L^

其中，S是一套符号集;b是底（或者基数）,它等于S符号集中的符号（数码）总数，其中Sk和SL分别代表整个数字或者小数部分的符号。注意我们使用的表达式可以从右边或者左边扩展。也就是说，b的幂可以从一个方向由0到K-1，也可以从0一个方向由-1到-L。b的非负数幂与该数字的整数部分有关，而负数幂与该数字的小数部分有关。+-符号表示该数字可正可负

十进制系统:

首先讨论的位置化系统是 十进制系统 。在该系统中，底b=10 并且我们用10个符号来表示一个数。符号集是 {0,1,2,3,4,5,6,7,8,9}
正如上文所说，该系统的符号常被称为“十进制数码”或者仅称为数码。暂时我们使用+-来表示一个数符号，但这些符号并不存储于计算机中——计算机处理该符号的方式不同，以后再提

在十进制系统中，数字写为:

+-(Sk-1….S2S1S0.S-1S-2S-L)10

为了简便，通常省略括号，底和正号。例如将+(552.23)表示为552.23,底和+是隐式存在的。

1.整数:

在十进制系统中，整数（没有小数部分的数字）是我们所熟悉的，在日常生活中使用整数。使用它我们已习以为常。我们把整数表示为 **+-(Sk-1…S1S0)10**，其值计算为:

N=+-Sk-1*10^k-1^+Sk-2*10^k-2^…+S0*10^0^

其中,Si是一个数码，b=10为底，K是数码的数量。

最大值:

有时我们需要知道可以用数码K表示的十进制数整数的最大值。答案是Nmax=10^K^-1

二进制系统:

讨论的第二种位置化数字系统是二进制系统。在该系统中，底b=2, 并且用两个符号来表示一个数，即S={0,1}。数据与程序都是以二进制模式（即位串）存储于计算机中的。这是因为计算机由电子开关制成，它们仅有开和关两种状态。位1表示这两状态之一，位0表示另一种状态。

1.整数:

可以把整数表示为 **+-(Sk-1…S1S0)2**，其值计算为:

N=+-Sk-1*2^k-1^+Sk-2*2^k-2^…+S0*2^0^

其中,Si是一个数码，b=2为底，K是数码的数量

2.实数:

在二进制系统中，一个实数（可带有小数部分的数字）可以由左边的K位和右边的L位组成，即 +-(Sk-1…S1S0.S-1S-L)2
其值计算为:

N=+-Sk-1*2^k-1^+Sk-2*2^k-2^…+S0*2^0^+S-1*2^-1^….+S-L*2^-L^

其中,Si是一个数码，b=2为底，K是小数点左边位的数量，L是小数点右边位的数量。注意: K从0开始，L从-1开始。最高的幂是K-1且最低的幂是-L。

例:

以下显示了与十进制数5.75等值的二进制数(101.11)2。
B = 1 0 1 · 1 1
R = 1x2^2^ + 0x2^1^ + 1x2^0^ + 1x2^-1^ + 1x2^-2^

转换

我们需要知道如何将一个系统中的数字转换到另一个系统中等价的数字。因为我们有十根手指，于是我们在日常中使用十进制数，通常看一个位置系统中的数字，我们大概率也是想要知道他在十进制中是什么数，那么先看看怎么从其他进制转到十进制吧。

从其他进制到十进制的转换

这种转换是简便而迅速。我们将数码乘以其的位置量并求和来得到在十进制中的数，如图:

十进制到其他进制的转换

我们能将十进制数转换到与其等价的其他进制需要两个过程。一个用于整数部分，一个用于小数部分。
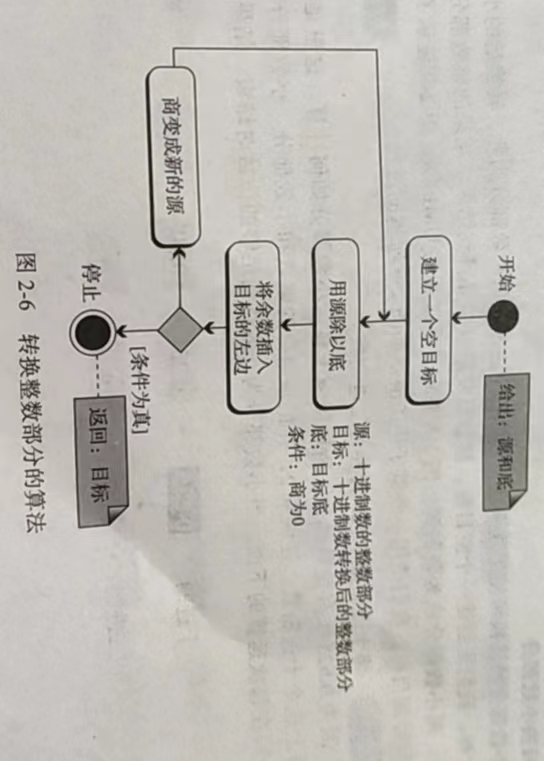
转换整数部分:
整数部分的转换可使用连除

一些例子：

转换小数部分:
小数部分的转换使用连乘法
如图，将十进制数0.625转换为二进制数

因为0.625没有整数部分，该例子很好的表现了连乘法的过程。左边是十进制数，连续乘2，并记录结果的整数部分和小数部分。小数部分移到右边作为新的源，整数部分写在每次运算的下面，当小数部分为0或达到足够的位数时停止。结果是（0.101）2