什么是堆栈?

堆栈是一种线性结构，也是一种特殊的线性表；堆栈在计算机学科中有着广泛的应用，如函数调用,递归,表达式求值等（考虑一下游戏中ui界面的调用，打开商城选择商品会蹦出来一个“结算”的子界面，此时玩家按下esc，该关掉哪个呢？肯定是遵守先进后出的原则先关掉结算界面吧，这就是堆栈的应用了）
思考一下计算机表达式求值的问题，如对于以下这个式子

5+6/2-2*4

正确理解是:

5+3-2*4 = 8-8 = 0

由两类对象构成的:

运算数,如2,4,5
运算符号,如+,-,*,/

由于不同运算符号优先级不同，使得求解变得较为复杂，而归根结底原因是我们把表达式把运算符号放在运算数中间
反过来，如果我们在遇到运算符号时已经知道两个运算数了，那么就简单许多了吧，这种表示叫 后缀表达式，在平常我们习惯使用的名为 中缀表达式
image.png

后缀表达式求值策略: 从左到右扫描，逐个处理运算数和运算符号

按照这种策略，我们需要一种数据结构来有效的组织,记住运算数;当需要运算时能取得最后两个记住的运算数。
这样的数据结构有一个特点，先存入的后取出，后存入的先取出，这实际上就是 堆栈
比如表达式

6 2 / 3 - 4 2 * +

它的求值过程如图
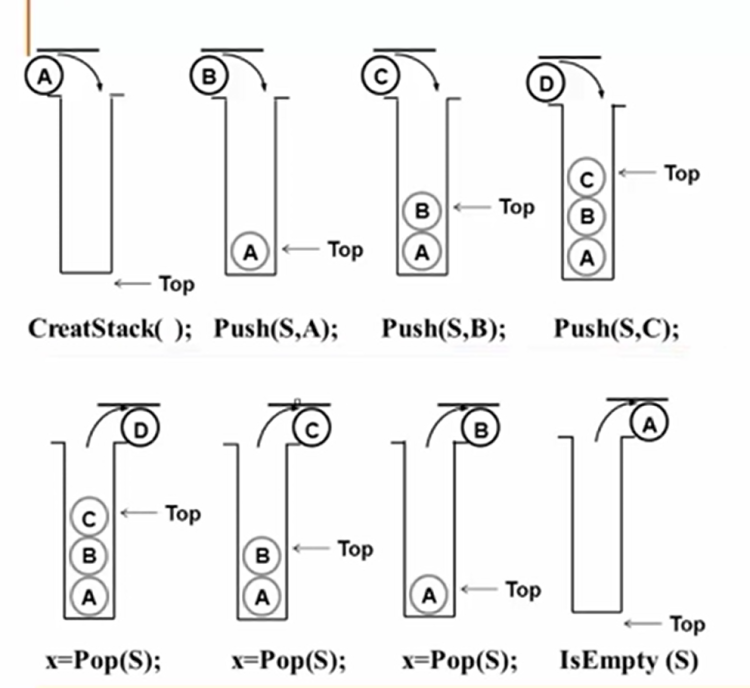
image.png
它是一个受约束的线性表，只能在一端（栈顶）进行插入与删除，插入我们称为入栈，删除数据为出栈
image.png
堆栈的操作流程图
image.png

顺序存储

既然它是线性表，很自然而然的我们可以用数组来实现

1
2
3
4
5
6
7
8
#include <iostream>
using namespace std;
const int MAXSIZE = 1000;
typedef struct SNode *Stack;
struct SNode{
	char data[];
	int top;
};

top用于记录栈顶的位置，实际上代表了栈顶位置的数组下标

插入与删除操作:

1.入栈

1
2
3
4
5
6
7
void push(Stack stack,char item){
	if(stack->top==MAXSIZE-1){
		printf("堆栈满");
		return;
	}
	stack->data[++(stack->top)] = item;
}

2.出栈

1
2
3
4
char pop(Stack stack){
	if(stack->top==-1) return NULL;
	return stack->data[(stack->top)--]
}

链表实现堆栈

线性表可以使用链表实现，堆栈作为一个特殊的线性表当然也可以；栈的链式存储结构实际上就是一个单链表，叫做链栈。插入和删除操作指南在链栈的栈顶进行。
那么问题来了，栈顶指针top应该定义在链表的哪一头呢？
答案当然是头结点，别忘记这是单链表，无法寻找到上一个节点，当我们用尾结点作为top时，删除操作是无法进行的（双链表当然可以，但要为此多写一些代码，和初衷不符）

1
2
3
4
5
typedef struct SNode *Stack;
struct SNode{
	char data;
	struct SNode *next;
};

我们定义CreateStack函数来生成一个空的堆栈

1
2
3
4
5
Stack createStack(){
	Stack s = (Stack)malloc(sizeof(struct SNode));
	s->next = NULL;
	return s;
}

根据代码，我们知道当头节点next指向NULL时为空栈

1
2
3
bool isEmpty(Stack s){
	return s->next==NULL;
}
入栈操作
1
2
3
4
5
6
void push(char item,Stack stack){
	struct SNode * tmpCell = (struct SNode *) malloc(sizeof(struct SNode));
	tmpCell->data = item;
	tmpCell->next = stack->next;
	stack->next = tmpCell;
}
出栈操作
1
2
3
4
5
6
7
8
9
char pop(Stack stack){
	if(isEmpty(stack))return NULL;
	struct SNode * firstCell = stack->next;
	stack->next = firstCell->next;
	char topItem = firstCell->data;
	free(firstCell);
	return topItem;
}

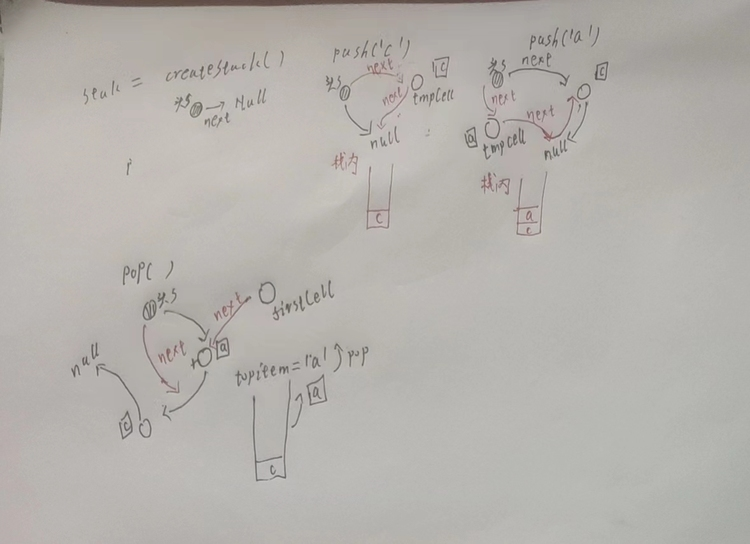
以下是进行

Stack stack = createStack();
push(‘c’,stack);
push(‘a’,stack);
cout << pop(stack);

操作的链表状态过程
image.png
输出结果为

a

表达式问题

现在回过头来看前面的表达式问题，现在我们可以很方便的实现后缀表达式；但我们更关心的是我们更常使用的中缀表达式，既然前者的运算更加方便，那么有没有办法进行转换呢？
观察一个简单的例子: 2+9/3-5 -> 2 9 3 / + 5 -
不难发现如下定义的规则:

1.运算数相对顺序不变
2.运算符号顺序发生改变
2.1 需要存储“等待”中的运算符号
2.2 要将当前运算符号与“等待中”的最后一个运算符号比较

模拟一下这个过程:
从左到右扫描这个表达式，遇到运算数时直接输出，在第二次扫描碰到了+号，能不能输出呢？显然是不行的，后面/的优先级更高，那么+入栈，输出9，此时输出的结果:

2 9

栈中的元素

+

继续扫描，遇到了“/“ ,能不能输出呢？此时需要和栈顶元素进行比较，/的优先级比+高，无法保证是安全的，/入栈，输出3;此时栈中元素为

/
+

接下来碰到了最后一个运算符-，和栈顶元素对比，-的优先级比/低，那么可以出栈了，此时输出结果为

2 9 3 / +

“-”入栈，扫描并输出最后一个运算数5，到尾了，将栈中元素全部输出。
那么中缀表达式 “2+9/3-5”的后缀表达式为:

2 9 3 / + 5 -

有括号怎么办？
比如对于表达式 *a(b+c)/d **,出现了括号，该这么进行转换呢;基本策略跟无括号时一样，但要记住:
对于左括号”(“ 在栈外时优先级高于任意运算符，在栈内时优先级最低;扫描过程中遇到右括号”)”时,
取出栈内”)”以上的所有元素
总结一下，我们得到了这样的流程:
image.png
可以看到，为了进行方便的转换，我们需要一种结构来按顺序保留运算符号，在需要的时候取出，当然就是 **堆栈 **了