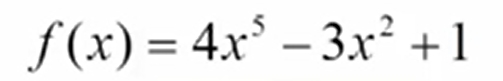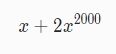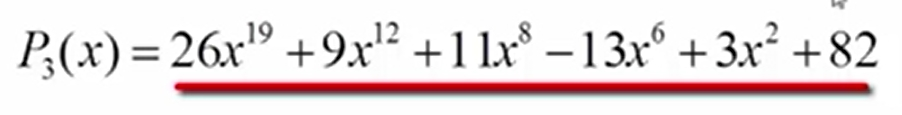<线性结构>笔记目录

线性表的实现与多项式表示 http://www.zsenhe.com/article/83
堆栈与表达式求值问题 http://www.zsenhe.com/article/84
队列，顺环队列 http://www.zsenhe.com/article/85

引子——多项式表示

线性结构是数据结构里最基础，最简单的一种类型;其中最典型的便是“线性表”，什么是线性表呢?
考虑一下一元多项式的表示:
image.png
这样的多项式基本运算包括: 两个多项式相加，相乘，相减等;那么，怎么用程序设计语言来表示这样一个多项式及运算呢?在程序设计语言里面，要表示一个问题，首先要分析一下问题的关键数据和关键信息;对于多项式而言，它的关键信息主要有它的项数和最高指数。
其中一种最简单的方法便是 顺序存储的直接表示
直接使用一个数组来表示多项式的有关信息，数组各分量对应多项式各项

a[i] 项 x^i 的系数;i为对应的指数

比方对于下面这个多项式:
image.png
表示为:
image.png
这样用6个分量来表示该多项式;这样的表示是很简单的，且运算也方便
如对于两个多项式的相加，即变成了 两个数组对应分量的相加
但该表示方式也是有问题的，如果我们要存储
http://cdn.zsenhe.com/QQ%E5%9B%BE%E7%89%8720230129004327.jpg
那么需要2001长度的数组来表示，而这2001个分量，只有两项是非0的，于是便造成了巨大的空间浪费;且运算的时候会多一些没必要的操作（大量的+0）

有没有可能只表示非0项呢？我们可以将多项式看成一个由 系数和指数 组成的二元组集合，使用结构数组来表示这样的多项式
image.png
对于前面的x+2x^2000,只需要使用两个分量来存储;且同样运算很方便，其中要点是每一项按指数大小降序存储
例如加法运算，图中的两个多项式，他们用分量表示为
p1:

(9,12) (15,8) (3,2)

p2:

(26,19) (-4,8) (-13,6) (82,0)

从头开始，比较两个多项式当前指数较大的那一项，例如第一项选择 (9,12) 与(26,19),前面提过我们需要按照指数大小降序排放，那么选择较大那一项输出(26,19),接下来(9,12)与(-4,8)比较，显然输出（9,12) ;接下来比较的两个分量指数相同，系数相减，输出和（11,8），接下来的比较输出(-13,6) (3,2);最后是p2的剩余项(82,0)
最后得到新的多项式
image.png
对比一下，我们使用结构体的形式存储在数组中表示非0项，这是一种节省空间的方法
当然，我们也可以使用一种其他形式存储多项式 链表
它的表示方法为: 每个节点存储多项式中的一个非0项，包括系数和指数两个数据域以及一个指针域
image.png

1
2
3
4
5
6
typedef struct PolyNode *Polynomial;
struct PolyNode {
  int coef; //系数
  int expon; //指数
  Polynomial link; //指向下一项
}

前面的两个多项式，他们以链表的形式存储状态为：
image.png
运算的逻辑过程与数组表现的形式一样

线性表

由多项式的问题得知: 同一个问题可以有不同的表现方法，也就是不同的存储方法；对于多项式的表示，要么使用数组要么使用链表。实际上很多问题与多项式表示是有共性的，我们的最终目标都是：管理，组织一个有序的线性序列，归结为线性表问题

什么是线性表?

由同类型数据元素构成有序序列的线性结构:
表中元素个数称为线性表的 长度
线性表没有元素时称为 空表
表起始位置称 表头，表结束位置称 表尾

对线性表来说，它的抽象数据类型描述为:
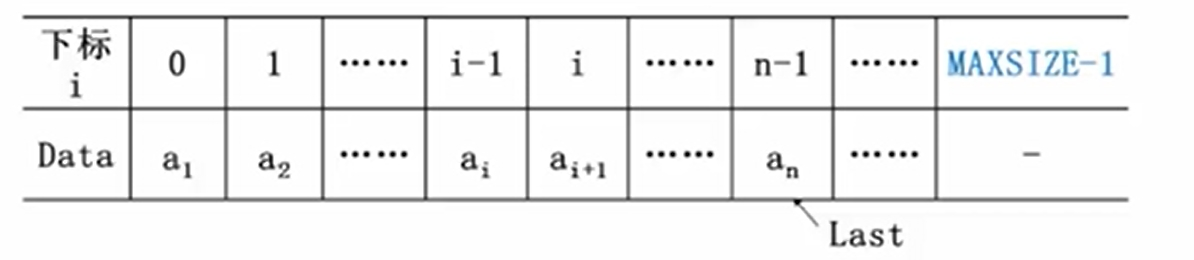
image.png

线性表的存储

学习数据结构时我们最关心的是它的存储，对于线性表的存储其中最简单的一种方式便是顺序存储，即使用数组的方法实现
image.png
这种方式需要关心的是线性表的 数据类型 以及 长度

1
2
3
4
5
struct LNode{
    ElementType data[MAXSIZE];
    int last;
}
struct LNode L;

使用指针last代表线性表的最后一个元素,访问长度时执行 L.last+1
这样的结构就可以抽象的实现线性表,比如说当想要访问下标为i的元素时使用 L.Data[i]

主要操作的实现

为了方便，我们使用指针来传递线性表

1
2
3
4
5
6
7
8
#include <iostream>
using namespace std;
const int MAXSIZE = 1000;

struct LNode{
  	char data[MAXSIZE];
  	int last;
};typedef LNode *List;

1.初始化操作

1
2
3
4
5
6
List MakeEmpty(){
  	List Ptrl;
  	Ptrl = (List )malloc(sizeof(struct LNode));
  	Ptrl->last = -1;
  	return Ptrl;
}

注意初始化时表长度为-1，即表示数组长度为0
2.查找操作

1
2
3
4
5
6
int Find(char x,List Ptrl){
  	int i=0;
  	while(i<=Ptrl->last&&Ptrl->data[i]!=x) i++;
  	if(i>Ptrl->last) return -1; //未寻找到
  	return i; 
}

从0开始遍历表，当while循环退出时，要么i==ptrl->last+1要么data[i]=x，这两种情况分别对应着 未寻找到元素 和 找到元素 它的时间复杂度显然为O(n)
3.插入
插入的目的是在线性表的第i个位置上插入一个新的元素，传入的i指的是[1,last+1] (1即是表头，last+1表尾);所以实际上我们要把元素插入到i-1的位置上
image.png
那么首先要做的就是把i-1之后的所有元素往后挪动一位，我们用一个循环来做这件事

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void Insert(char x,int i,List Ptrl){
  	if(Ptrl->last==MAXSIZE-1){
    		//表空间已满，无法插入
    		printf("full");
    		return;
  	}
  	if(i<1||i>Ptrl->last+2){
    		printf("位置不合法");
    		return;
  	}
  	for(int j=Ptrl->last;j>=i-1;j--) //从右开始挪动元素
    		Ptrl->data[j+1] = Ptrl->data[j];
  	Ptrl->data[i-1] = x; //插入新元素x
  	Ptrl->last++; //last仍指向最后一个元素
  	return;
}

该操作的时间复杂度依然是O(n)
4.删除元素
我们要把第i-1个元素移出，那么实际上要做的把i及之后的元素全部往前挪，这个过程按从左往右的顺序做

1
2
3
4
5
6
7
void Delete(int i,List Ptrl) {
  	if(i<1||i>Ptrl->last+1) return; //判断位置是否合法 
  	for(int j=i;j<=Ptrl->last;j++) 
    Ptrl->data[j-1] = Ptrl->data[j];
  	Ptrl->last--; 
  	return; 
}

链式存储

线性表除了用数组实现，同样可以使用链表来组织
线性表使用数组实现时，两个相邻的元素不止逻辑上是相邻的，在物理上也是相邻的（数组在内存中也是连续存放的一片空间）；而我们使用链表实现时，实际上是要求两个元素只在逻辑上相邻（通过“链”建立），而不要求物理上相邻
这样的好处是进行插入，删除操作时，只需要修改“链”的指向，而不需要像数组实现那样移动整个空间，这会节省很多时间
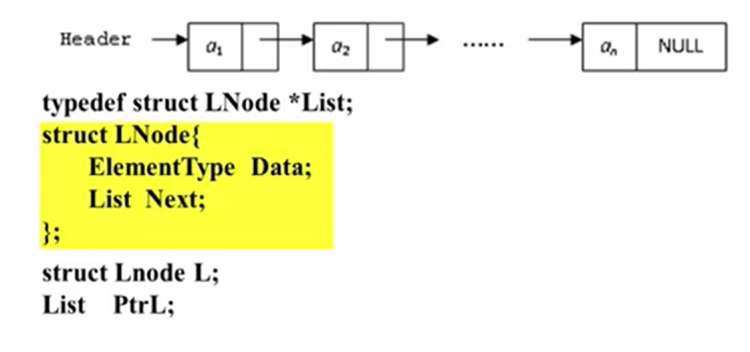
image.png

1
2
3
4
5
6
7
#include <iostream>
using namespace std;
typedef struct LNode *List;
struct LNode{
	char data;
	List next;
};

如图，链表中每个节点拥有两个分量，Data是节点所对应的数据，Next指向下一个节点

访问序号为i的元素?求线性表的长度？

上文提到链实现线性表在插入删除方面有着数组无可比拟的高效,那除此之外呢?在数组实现中访问序号为i的元素是很简单的事，直接ElelementType[i-1]即可;同样，我们也可以直接取last来知道线性表的长度.但在链表中，这两个操作比起数组实现就复杂了许多
求表长

1
2
3
4
5
6
7
8
9
int length(List ptrl){
  	List p = ptrl; //指向链表头结点 
  	int j = 0;
  	while(p){ //当next指向null时退出循环（代表已经走到最后一个节点  了 
  		p = p->next;
  		j++;
  	}
  return j;
}

因为需要遍历整个链表，它的时间复杂度为O(n);在数组实现中该操作是O(1)的
按序号访问节点

1
2
3
4
5
6
7
8
9
10
List findKth(int k,List ptrl){
	List p = ptrl; //指向头结点 
	int i=1;  
	while(!p&&i<k){
		p = p->next;
		i++;
	}
	if(i==k) return p; //p不为null意味着找到了这个节点 
	return NULL;
}

当while循环退出时，意味着!p或者i<k这两个条件之一被破坏了，当p不为null时，即找到了目标节点
按值查找

1
2
3
4
5
List findKth0(char target,List ptrl){
	List p = ptrl;
	while(!p&&p->data!=target) p = p->next;
	return p;
}

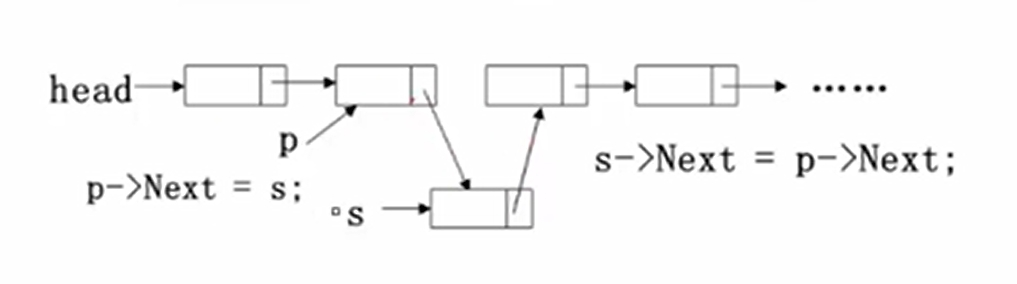
插入与删除

插入
将数据插入到i的位置上，意味着我们要将数据插入到i-1的后面，为了完成这个操作
我们需要进行以下几个步骤的操作

1.申请一片新的内存，使用s指向它
2.找到链表的i-1个节点，使用p指向
3.修改指针，插入节点
image.png
修改指针的动作有两步，将s->next指向p->next,再将p->next指向s(注意不要搞反)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
List insert(char x,int i,List ptrl){
	List p,s;
	if(i==1){
		s = (List)malloc(sizeof(struct LNode));
		s->data = x;
		s->next = ptrl;
		return s;
	}
	p = findKth(i-1,ptrl);
	if(p==NULL){
		//第i-1个节点不存在，无法插入 
		return NULL;
	}
	s = (List)malloc(sizeof(struct LNode));
	s->data = x;
	s->next = p->next;
	p->next = s;
	return ptrl;
}

删除
删除同理是对指针的修改，同样的使用p指向i-1,申请一个新的指针s指向p->next,最后将p->next指向s->next即可；通过malloc申请的空间要记得free回去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
List Delete(int i,List ptrl) {
	List p,s;
	if(i==1){ //当要删除表头节点时 
		s = ptrl; //指向第一个节点 
		if(ptrl!=NULL) ptrl = ptrl->next; //从链表中删除 
		else return NULL;
		free(s);
		return ptrl;
	}
	p = findKth(i-1,ptrl);
	if(p==NULL){
		//i-1个位置不存在 
		return NULL;
	}else if(p->next==NULL) return NULL; //第i个位置不存在 
	s = p->next;
	p->next = s->next;
	free(s);
	return ptrl;
}

完整的代码存档:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <malloc.h>
using namespace std;
const int MAXSIZE = 1000;
struct LNode{
	char data[MAXSIZE];
	int last;
};typedef LNode *List;


//建表 
List MakeEmpty(){
	List Ptrl;
	Ptrl = (List )malloc(sizeof(struct LNode));
	Ptrl->last = -1;
	return Ptrl;
} 


//查找 
int Find(char x,List Ptrl){
	int i=0;
	while(i<=Ptrl->last&&Ptrl->data[i]!=x) i++;
	if(i>Ptrl->last) return -1; //未寻找到
	return i; 
}

void Insert(char x,int i,List Ptrl){
	if(Ptrl->last==MAXSIZE-1) return;
	if(i<1||i>Ptrl->last+2) return;
	for(int j=Ptrl->last;j>=i-1;j--)
		Ptrl->data[j+1] = Ptrl->data[j];
	Ptrl->data[i-1] = x;
	Ptrl->last++;
	return;
} 

//删除
void Delete(int i,List Ptrl) {
	if(i<1||i>Ptrl->last+1) return; //判断位置是否合法 
	for(int j=i;j<=Ptrl->last;j++) Ptrl->data[j-1] = Ptrl->data[j];
	Ptrl->last--; 
	return; 
}
int main(){
	List L = MakeEmpty();
	Insert('a',1,L);
	cout << Find('b',L);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <iostream>
#include <malloc.h>
using namespace std;
typedef struct LNode *List;
struct LNode{
	char data;
	List next;
};

int length(List ptrl){
	List p = ptrl; //指向链表头结点 
	int j = 0;
	while(p){ //当next指向null时退出循环（代表已经走到最后一个节点了 
		p = p->next;
		j++;
	}return j;
}

//查找操作 （按序号 
List findKth(int k,List ptrl){
	List p = ptrl; //指向头结点 
	int i=1;  
	while(p&&i<k){
		p = p->next;
		i++;
	}
	if(i==k) return p; //p不为null意味着找到了这个节点 
	return NULL;
}

//按值查找 
List findKth0(char target,List ptrl){
	List p = ptrl;
	while(p&&p->data!=target) p = p->next;
	return p;
}

//插入
List insert(char x,int i,List ptrl){
	List p,s;
	if(i==1){
		s = (List)malloc(sizeof(struct LNode));
		s->data = x;
		s->next = ptrl;
		return s;
	}
	p = findKth(i-1,ptrl);
	if(p==NULL){
		//第i-1个节点不存在，无法插入 
		return NULL;
	}
	s = (List)malloc(sizeof(struct LNode));
	s->data = x;
	s->next = p->next;
	p->next = s;
	return ptrl;
} 

//删除
List Delete(int i,List ptrl) {
	List p,s;
	if(i==1){ //当要删除表头节点时 
		s = ptrl; //指向第一个节点 
		if(ptrl!=NULL) ptrl = ptrl->next; //从链表中删除 
		else return NULL;
		free(s);
		return ptrl;
	}
	p = findKth(i-1,ptrl);
	if(p==NULL){
		//i-1个位置不存在 
		return NULL;
	}else if(p->next==NULL) return NULL; //第i个位置不存在 
	s = p->next;
	p->next = s->next;
	free(s);
	return ptrl;
}
struct LNode L;
List Ptrl;
int main(){
	return 0;
}