队列也是一种受操作约束的特殊线性表;进行插入和删除操作的时候 只能在一端插入，而在另一端删除
它的插入和删除操作分别发生在表的两头，而一般化的线性表可以在任何位置进行插入和删除
数据的插入我们称之为 入队(AddQ) ;删除称为 出队(DeleteQ)
这种表又被称为 先入先出表
抽象数据类型描述为:
image.png
队列的存储实现一样有两种方式,顺序存储与链式存储;顺序存储的实现如下

1
2
3
4
5
6
7
8
9
10
11
#include <iostream>
using namespace std;
const int MaxSize = 1000;
struct QNode {
	char data[MaxSize];
	int front,rear;	
};
typedef struct QNode *Queue;
int main(){
	return 0;
}

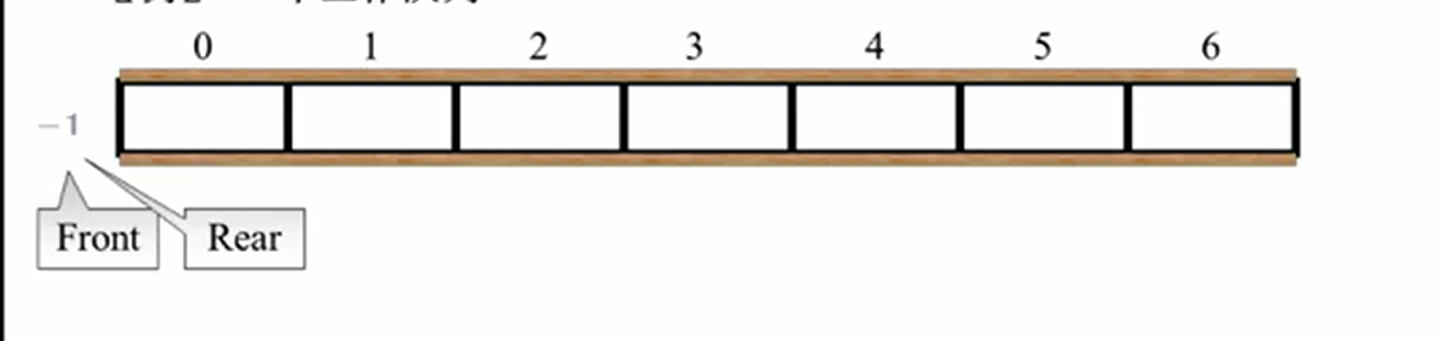
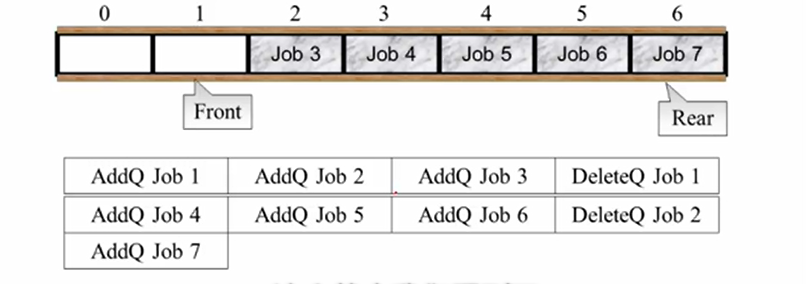
对比堆栈，它只在表的一端进行插入删除，只需要一个top分量;而队列需要使用两个分量 front,rear 分别表示队列的队头和队尾
image.png
在一开始,front,rear指针都指向-1这个下标，队列是空的
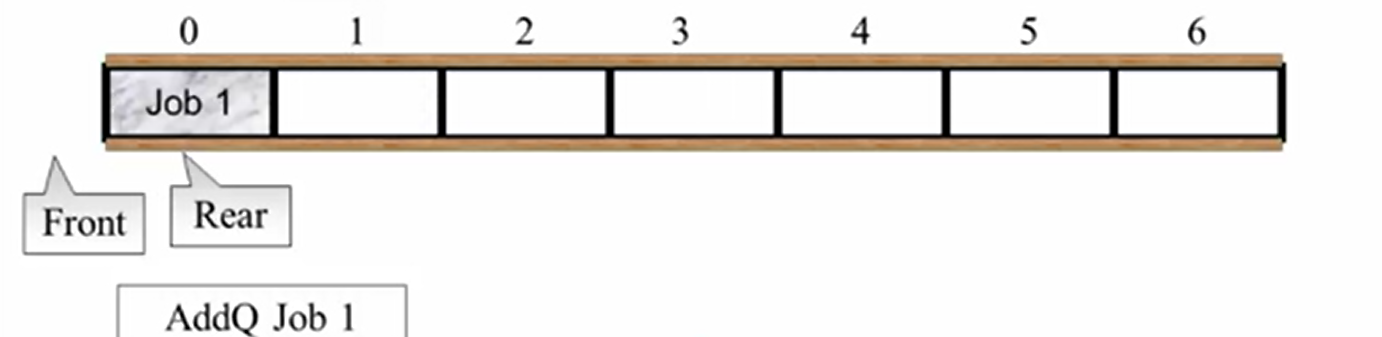
image.png
加入一个元素，rear往后挪动指向0
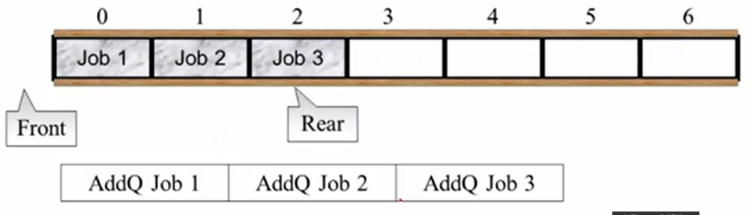
image.png
重复这个过程，此时rear指向下标2。
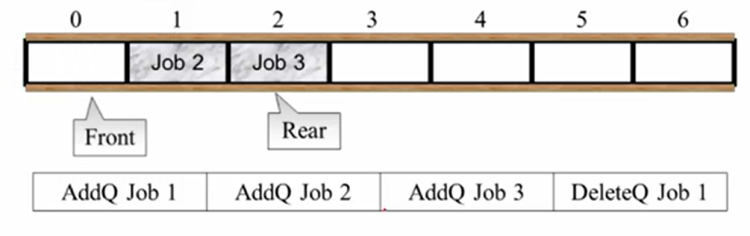
接下来，我们想要删除一个元素，依照队列的原则，先被弹出的是Job1这个元素。注意到在删除之前front仍然指向-1，实际上front是指向队列的头一个元素再前面的下标
image.png
指向出队操作，Job1出队，front向后移; 综上，入队rear+1，出队front+1

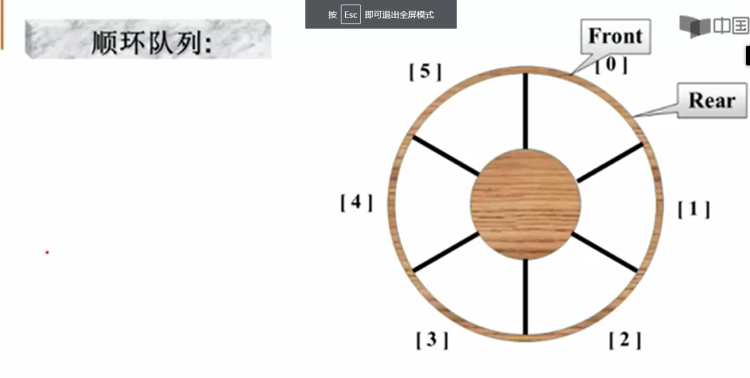
顺环队列

image.png
队列中时常会有这样的状态，数组尾部加满了，但前面已经有元素出队;rear无法再往后移，但数组前面还有空闲资源。那怎么办呢？重新开辟一个更大的数组势必要有元素移动等操作，我们可以用 顺环队列
image.png
一开始的时候，front，rear两个指针都指向某个位置，front==rear时队列是空的
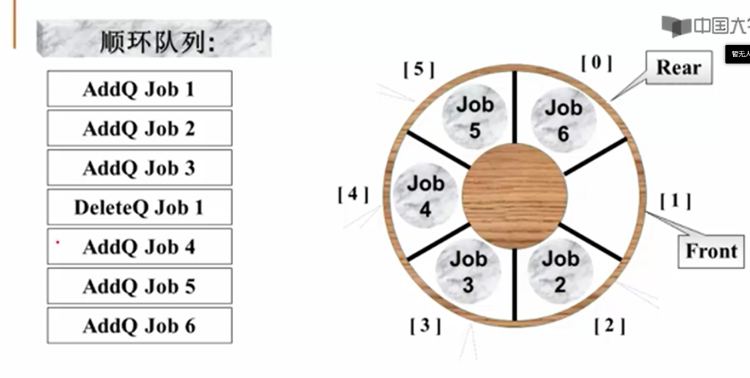
image.png

指向队列的一般操作，此时队列来到了这个状态，总共6个分量，此时已经有5个被占满了;这个时候，我们想再往里插入一个元素，加入之后rear+1=1,front也等于1，诶，根据前面的说法，front=rear时队列为空，但里面明明满满当当的元素啊这就矛盾了，当front==rear时，队列是空的还是满的呢？
根本原因在于，我们判别队列状态时，根据的是front和rear之间距离的相对关系来判断的，对于一个大小为n的队列，他们之间的差距有n种情况;而队列状态有几种情况呢？是n+1吧（空集也算一个)，而front和rear的差距只有n种情况，也就是说我们想使用n种的状态来区分实际上存在的n+1种情况
就像用一个bit来区分3种情况一样不可能，这就是它的根本原因；既然原因找到了，自然也有解决的方案

  1. 使用一个额外的tag来区分标记 (当入队的时候tag++，出队的时候tag–，以tag来判断队列的状态)
  2. 仅使用n-1个数组空间（如此对于n=3大小的数组，它的元素装载只有(0,1,2)三种情况)

最优雅的是采取第二种方案，对于入队操作，我们这样写

1
2
3
4
5
6
7
8
9

void addQ(Queue q,char item){
	if((q->rear+1)%MaxSize == q->front){
		printf("队列已满");
		return;
	}
	q->rear = (q->rear+1)%MaxSize;
	q->data[q->rear] = item;
}

使用求余来取得下一个存放的位置，当下一个位置与front碰上的时候，队列已经满了
对于出队操作:

1
2
3
4
5
6
7
char deleteQ(Queue q){
	if(q->front==q->rear){
		return NULL; //队列空 
	}
	q->front = (q->front+1)%MaxSize; 
	return q->data[q->front];
}