::: hljs-center

树与二叉树

:::
<树，二叉树结构> 笔记目录

0. 树与二叉树
1. 二叉树的定义与存储
2.二叉树的遍历

顺序查找

查找指的是根据某个给定关键词K，从集合R中找出关键字与K相同的记录，查找分为两类

静态查找: 集合中记录是固定的，没有插入删除操作，只有查找
动态查找: 集合中记录是动态变化的，除查找外还可能发生插入与删除操作

举个例子，一本词典中可能有成万上百万的单词，当它印刷成书的时候集合是不变的，我们经常需要进行单词的查阅，这就是所谓静态查找了;而动态查找可能发生在某个百科网站上，当我们检索条目的同时可能也有一些过时的资料被清除更新

我们的一般表示方法是把数据放在数组里面

1
2
3
4
5
6
const int N = 1001;
struct LNode{
	int data[1001];
	int length;
};
typedef LNode * L;

顺序查找这样写：

1
2
3
4
5
6
int findTarget(L l,int target){
	int i;
	l->data[0] = target; //建立哨兵 
	for(i = l->length;l->data[i]!=target;i--);
	return i;
}

哨兵?这是什么新术语

它的存在是为了少写一些边界判断的逻辑，我们定义一个“哨兵”将它存放在数组下标为0的位置，这样当循环退出时，i为0自然就是未找到了;于是我们知道接收到0的时候，就是元素不存在于数组中，当然这样实现的话，插入元素时需注意合法下标在 [1,n)
它的时间复杂度是 O(N)

二分查找

顺序查找的效率显然是极低的。我们可以使用二分查找（也叫折半查找）,它并不是生面孔，平常的聚会游戏也会经常用到，没有任何的改变
假设n个数据元素的关键字满足有序（降序 升序）并且连续存放,代码长这样

1
2
3
4
5
6
7
8
9
10
11
12
int binarySearch(L l,int target){
	int left,right,mid,NF = -1;
	left = 1;//初始化左边界 
	right = l->length; //初始化右边界 
	while(left<=right){ 
		mid = (left+right)/2; //计算中间元素坐标 
		if(target<l->data[mid])  right=mid-1; //调整右边界 
		else if(k>l->data[mid]) left = mid+; //调整左边界 
		else return mid;
	}
	return NF; //未查找成功，返回-1 
}

每次查找都缩小一半范围，实际意义即是n = n/2，根据公式知道除以logn次后归1，于是它的时间复杂度为 O(logn)
通过事先对数据进行排序，可以让我们的查找效率大大提高
对于二分查找的解题思路，这里有一篇很详细的笔记： 二分查找的思想和解题步骤笔记，模板

## 二分查找的启示

为什么二分查找就快呢？通过事先排好序，实际上我们已经构建了它的查找顺序;我们可以构造出这样的一棵树来表述
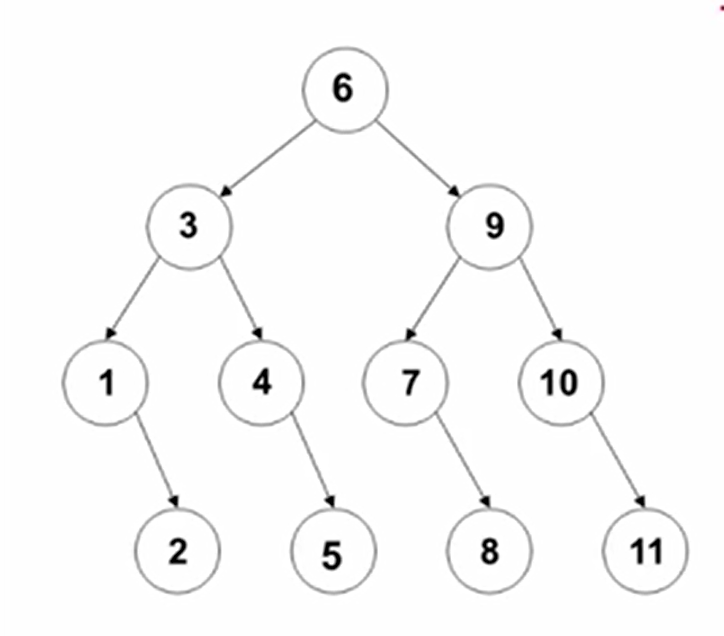
image.png

对于从1开始的这样11个元素，只要排好序了，那么第一次比较的一定是下标为6这个元素，根据查找的值来决定往左节点走还是右节点走，对于6这个位置，如果比较值元素比l[6]大，那么下一次将往右节点9走….以此类推

而元素的查找次数便是所在的层数,例如4这个节点是要寻找的值，它位于第三层，比较三次后就可以取出;树的总层次是logn+1,+1是为了取整;树的深度有logn+1层

考虑它的平均查找次数,树总共有4层

查找4次总共有4种情况,查找3次4种情况,查找2次2种情况，查找1次只有1种情况（l[6]==target）

那么它的平均查找成功次数 ASL = (4*4+4*3+2*3+1)/11 = 3
综上所述，由于我们在数组里面对查找的元素进行了有序化的组织，使得查找过程按照固定的顺序进行，而顺序形成了类似树的结构;那反过来说，我们能不能按照这一种树的结构来存储数据，能不能达到二分查找的要求?这就是查找树了，在效率上它可以和二分查找达到同样logn，同时它在插入数据时，比存储在数组中方便的多

以查找树的形式存储，可以很好的解决顺序查找的第二大类问题 动态查找问题

树的定义

树(Tree): n (n>=0) 个节点构成的有限集合。
当n=0时，称为 空树;
对于任一非空树(n>0)，它具备以下性质:

树中有一个称为根(root)的特殊节点,用r表示
其余节点可分为m(m>0)个互不相交的有限集T1,T2…Tm,其中每个集合本身又是一棵树，称为原来树的子树(SubTree)

image.png
树的定义采用了递归的设计，例如A是由下一层的四棵子树构成，每个子树又是一棵树

树与非树

image.png
如图，这样的结构为什么不能称之为树呢?前面提到了树的子树之间是不相交的，如图1由于C与D之间连着线，我们无法做到把他们切割开来

现在明确一下树的更多概念

1.子树是不相交的
2.除了根节点以外，每个节点有且仅有一个父节点
3.一颗N个节点的树有N-1条边
（因为每个节点都有一条通往父节点的线，root除外）

树是保证节点联通的最小的一种连接方式;即边最少的一种方式

树的一些基本术语

  1. 节点的度(Degree): 节点的子树个数
  2. 树的度: 树的所有节点中最大的度数
  3. 叶节点(Leaf): 度为0的结点
  4. 父节点(Parent): 有子树的结点是其子树根节点的父节点
  5. 子节点(Child): 若A节点是B节点的父节点，则称B节点是A节点的子节点;子节点也称孩子节点
  6. 兄弟节点(Sibling): 两个节点具有同一父节点，即称之为兄弟节点
  7. 路径和路径长度: 从节点N1到Nk的路径称之为一个节点序列(N1,N2…Nk-1,Nk),Ni是Ni+1的父节点。路径中包含的边数称为路径长度
  8. 祖先节点: 沿树根到某一节点路径上的所有节点都称为这个节点的祖先节点
  9. 子孙节点: 某一节点的子树中的所有节点都称之为这个节点的子孙节点
  10. 节点的层次: 规定根节点在1层，其他任一节点的层数是其父节点的层数+1
  11. 树的深度: 树中所有节点中的最大层次是这棵树的深度

大多数概念类似家谱系中的表示，完全可以用常识去理解加深印象

树的表示

考虑前面所学的知识，树能不能使用链表或者数据来实现呢？首先考虑数组，这样难度还是较大的，因为树中存在着很多形式，任何一个节点可能都有一个或多个儿子;我们很难判断一个节点的父节点是谁,儿子是谁

如果用链表来实现呢?它可能会长这样
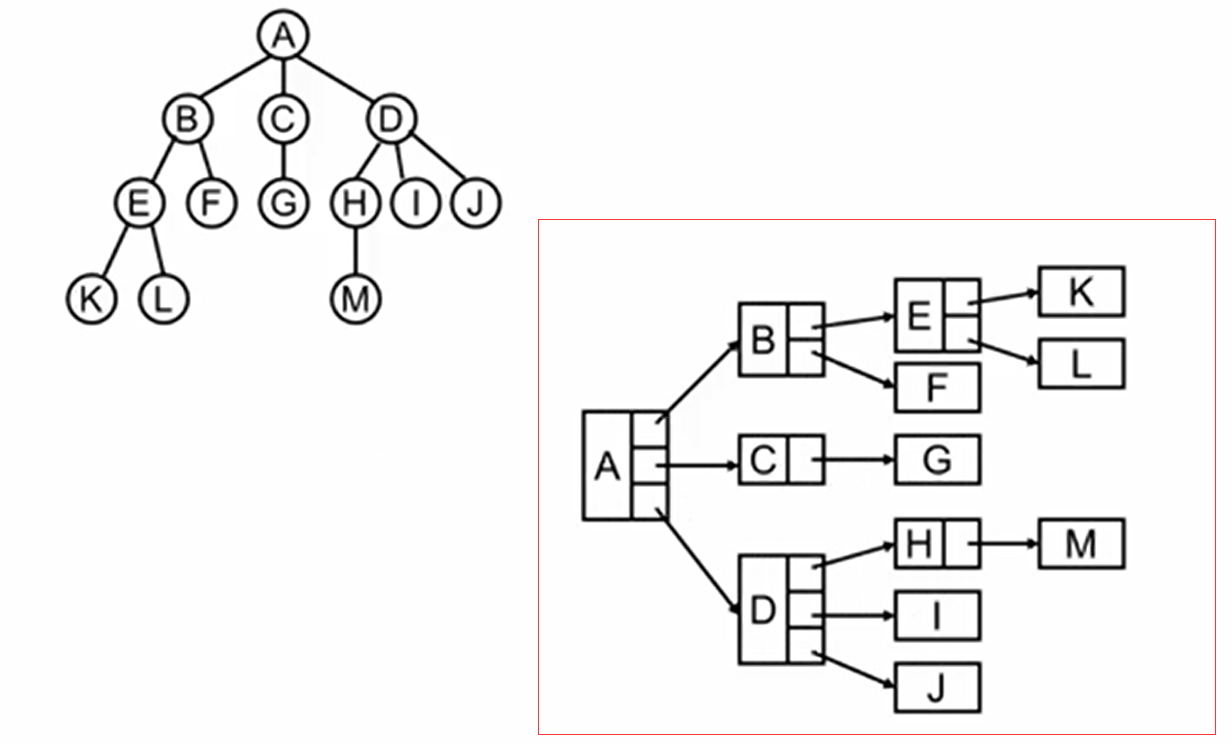
image.png
每个节点使用一个结构来表示,好像是没问题的,完全可以用结构加指针来表示一棵树?仔细观察,这种方式也是不完美的,如A节点有三个子节点,而B有两个子节点,他们的结构是不一样的,无法做到统一;结构的形式不一样会对程序设计带来困难，毕竟我们访问一个节点时，是无法事先知道他的子节点数量的

另外一种途径呢?把所有的节点设计成一样的结构,例如图中,树的度是3,那我们统一节点的结构,让每个节点都拥有3个指针不就行了,空的就指向NULL

这样解决带来了新的问题,如果这棵树有n个节点,那代表着每个节点拥有3个指针域,这意味着整个树拥有3n个指针;而树只有n-1条边,也就是说只有n-1个指针是非0的,这意味着会有2n+1个指针指向NULL,造成空间浪费

儿子-兄弟表示法

这是一种更好的表示方法，称之为: 儿子-兄弟表示法

它每个节点的结构如下:
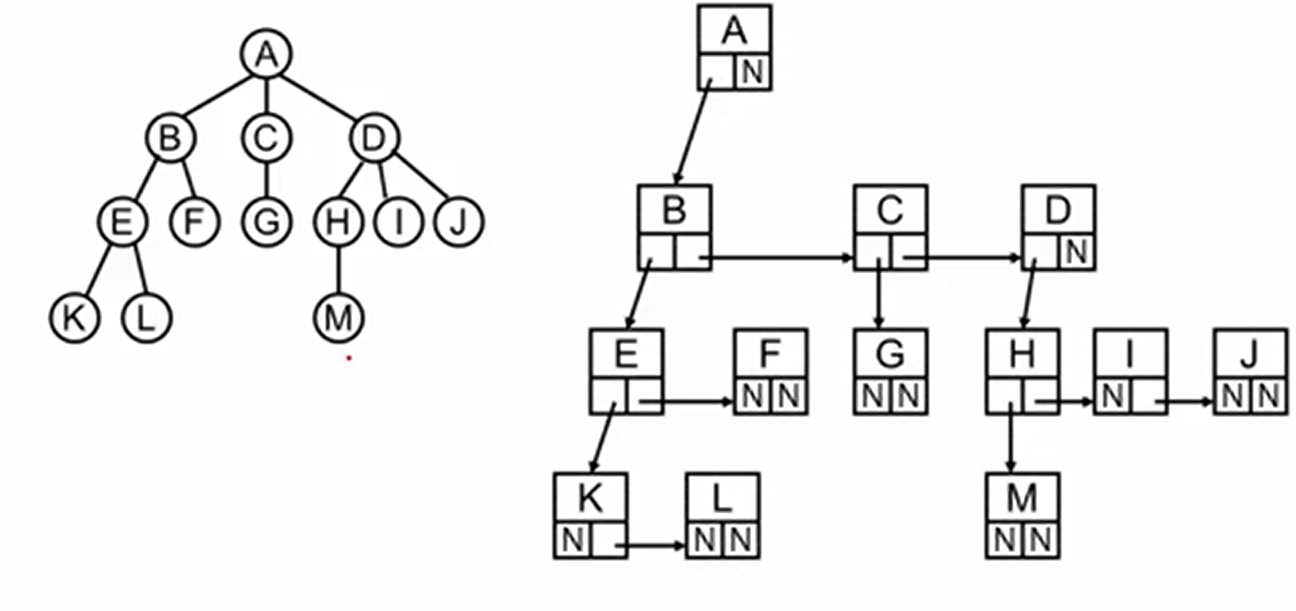
image.png

FirstChild 指向了它的下一个子节点; NextSibling 指向下一个兄弟节点。以此来把整棵树串起来

image.png

这样的表示方法使得树中的每个节点结构都是统一的且不会造成空间浪费(n+1个指针是空的)

将右图旋转45°得到:
image.png
形成一棵“树”，可以看到每个节点都有两个指针，最多有两个儿子，这种树称之为 二叉树 ;即树的度为2
综上，不管怎样的树结构，我们都可以用儿子-兄弟表示法，将它用二叉树链表的形式实现

所以，当我们想研究一般树的表示与操作的实现，如果我们搞清楚了二叉树的表示与实现，便解决了大部分问题;所以二叉树是树结构研究里面最重要最主要的内容

引用&参考:
树,数据结构[维基百科]