::: hljs-center

二叉树的存储与遍历

:::

二叉树的定义

二叉树T: 一个有穷的节点集合
这个集合可以为空;若不为空，则它是由根节点和称为其左子树Tl和右子树Tr的两个不相交的二叉树组成。
从某种角度理解，二叉树可以当做一颗度为2的树，但他有左右之分

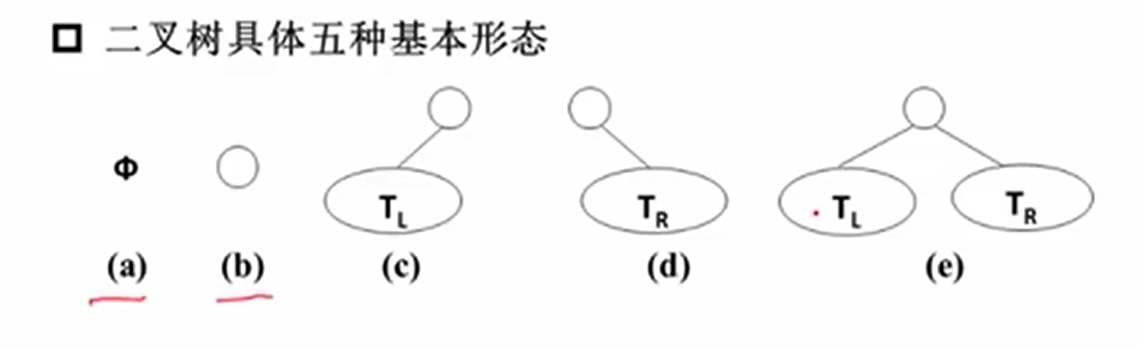
二叉树的五种基本形态

image.png

a : 空二叉树
b : 只有一个根节点
c d : 左右子树分别为空
e : 拥有左右子树

二叉树与一般树的差别便是子树拥有左右顺序之分，而一般度为2的树是没有左右之分的

特殊二叉树

斜二叉树

子树都往一边倒，只有左儿子，没有右儿子（当然也可能往右边倒）;这样的结构实际上就形成一个链表了
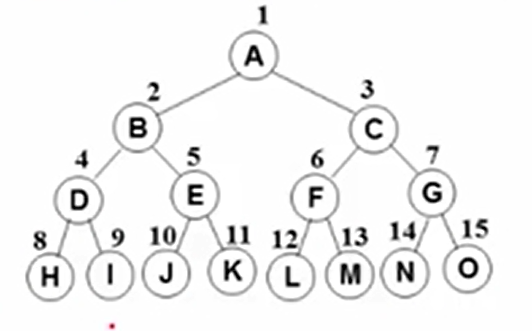
image.png

完美二叉树（满二叉树）

image.png
除叶节点外，每个节点都拥有左右子树，称之为完美二叉树

完全二叉树

有n个节点的二叉树，从上到下从左到右对节点进行编号，编号为i的节点与完美二叉树中编号i节点位置相同
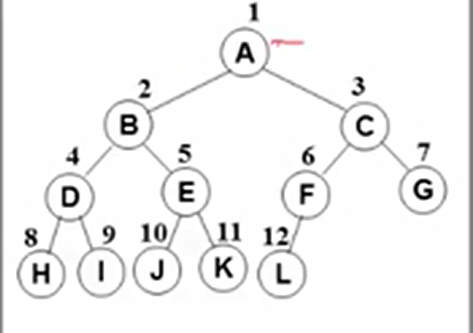
听起来有点绕，将上面的完美二叉树拿掉一些节点
image.png
可以看到，即使缺失了叶节点右边一部分，他的序号依然与满二叉树保持一致，这也能称之为 完全二叉树
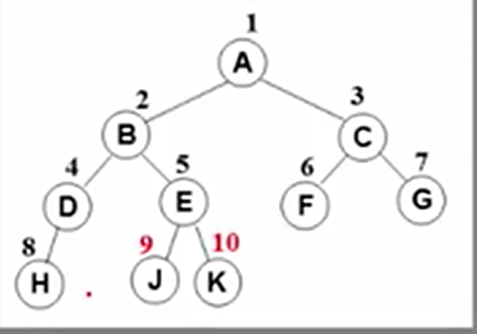
image.png
如图，因为节点D的右儿子缺失，使得编号与完美二叉树不一致，这就不能称为完全二叉树

二叉树的重要性质

  1. 一个二叉树第i层的最大节点数为 2^i-1^,i>=1
  2. 由1可以推出: 深度为k的二叉树拥有最大节点数量 2^k^-1,k>=1
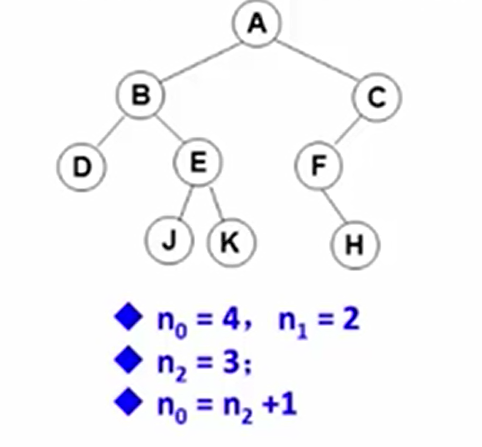
  3. 对于任何非空二叉树T，若N0表示叶节点个数,N1表示度为1的节点个数.N2表示度为2的节点个数，存在 n0=n2+1 的关系
    image.png

能证明这个结论吗?其实是不难的,对于一棵节点数为n的二叉树T，除根节点外对边数的贡献都为1，于是总的边数k=n-1;展开来说 k=n0+n1+n2-1。n1对于边的贡献为n00,n1的贡献为n11,n2的贡献为n2*2，得出以下等式关系:

n0+n1+n2-1 = k = n0*0 + n1 + 2n2
两边一约,推出:
n0 = n2+1
问题得证

二叉树的抽象数据类型定义

image.png
遍历是二叉树的主要操作，大多数算法实现都在此基础上，二叉树的遍历分为:

void PreOrderTraversal(T) 先序 根,左子树,右子树;
void InOrderTraversal(T) 中序 左子树,根,右子树;
void PostOrderTraversal(T) 后序 左子树,右子树,根;
void LevelOrderTraversal(T) 层次遍历 从上至下，从左到右;

二叉树的存储结构

顺序存储

根据前面的经验，我们想到有没有可能用数组来进行表示。前面提到过一般的树用数组实现是很困难的，但二叉树不同，它的度只有2，分支相对较少
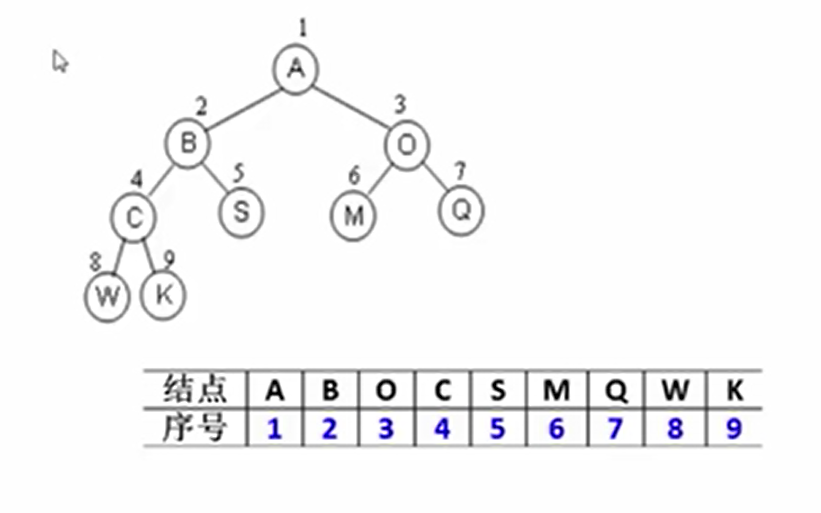
对于完全二叉树，由于节点是从上往下,从左到右编号,我们可以在数组中连续存放
image.png
对于这样的存放，他在数组中下标的映射有如下规律:

对于节点i:
根节点位于 i/2 ,向下取整
左儿子 2i;右儿子2i+1

一般二叉树同样可以使用数组存放,只是要对数组空间造成浪费
image.png

链表存储

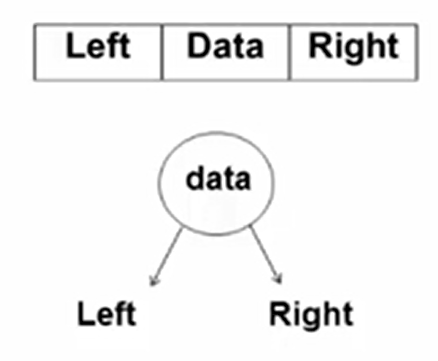
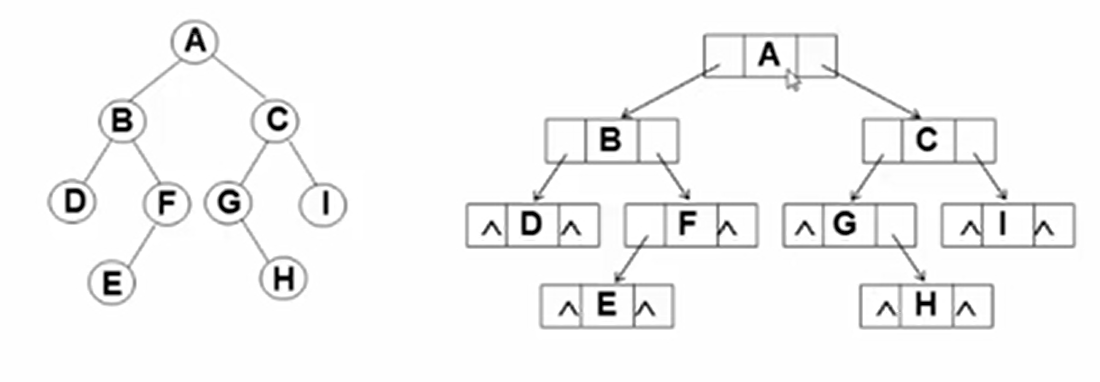
别忘记前面的儿子-兄弟表示法，使用两个指针域分别指向左右儿子就可以了
image.png

1
2
3
4
5
6
7
typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
	char data;
	BinTree left;
	BinTree right;
};

如图:
image.png

习题&错题整理

  1. 如果一个完全二叉树最底下一层为第六层（根为第一层）且该层共有8个叶结点，那么该完全二叉树共有多少个结点？
    解: 对于深度为6的完全二叉树，1-5层构成一棵完美二叉树T，T的节点数为2^5^-1 = 31，加上叶节点 31+8 = 39，于是答案为39