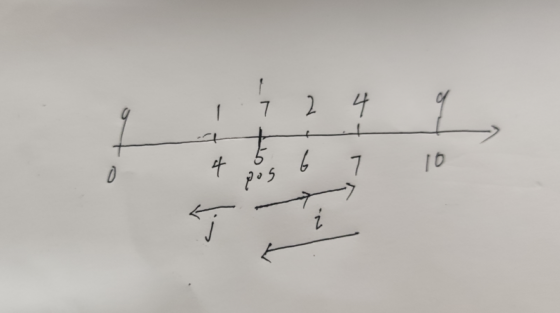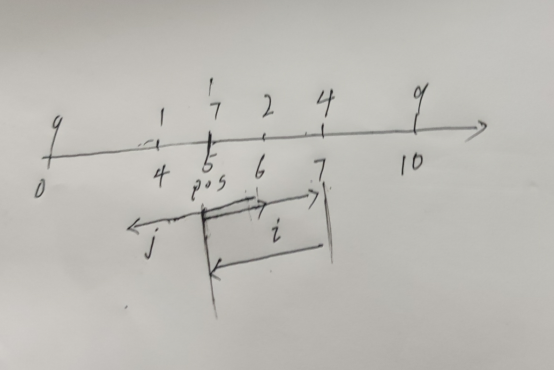image.png
image.png
一开始想的是二分去做,推了一些发现映射到坐标轴左右移动上太麻烦了。就转而用双指针了,被边界卡了一上午。整理下思路
首先需要明确的就是往一个方向移动后,最多回头一次,如果回头后再次转向只会浪费策略(既然要再次回头,那为什么不一次性往一条路走呢)
只要明白这一点,这题大概就能从hard降到中等了
如图,以样例2为例
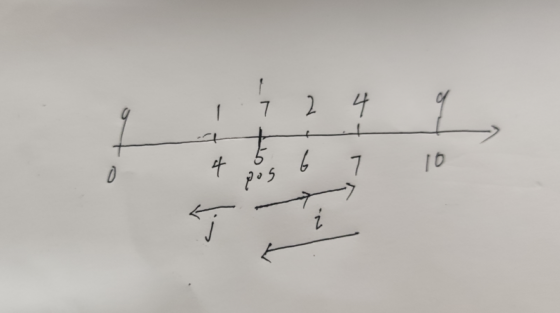 image.png
image.png
当i指针递增的时候,j也会随之往右拉,因为2(i-startPos)+(startPos-j)必须<=k,显然可以使用滑动窗口来操作
分别枚举以startPos上下界区分的左右两个区间即遍历所有的方案,在其中选择最大的即可。但要注意一些边界情况
如在枚举右窗口i指针时,j有可能越过startPos
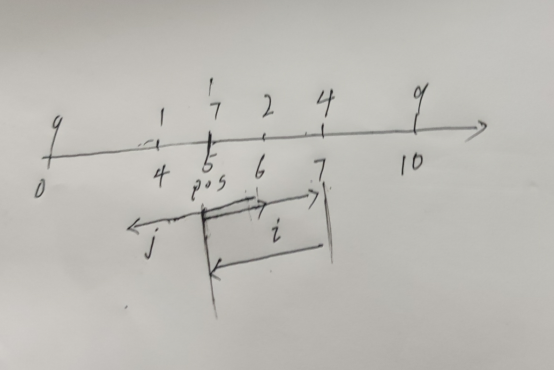 image.png
image.png
当发生这种情况的时候,(startPos-j)可以被丢弃,但(i-startPos)可能是有效的,需要特判一下。处理左窗口的时候同理
每次选取一对i,j后,在预处理好的前缀和中划分区域来得到采摘的水果数(推了好久)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class Solution {
private int lowerBound(List<Integer> pos,int x){
int l = 0,r=pos.size()-1;
while(l<r){
int mid = l+r>>1;
if(pos.get(mid)>=x) r=mid;
else l = mid+1;
}
return l;
}
public int maxTotalFruits(int[][] fruits, int startPos, int k) {
List<Integer> pos = new ArrayList<>();
int[] sum = new int[fruits.length];
for(int i=0;i<fruits.length;i++){
pos.add(fruits[i][0]);
sum[i] = (i==0?0:sum[i-1])+fruits[i][1];
}
int length = pos.size();
int mid = lowerBound(pos,startPos);
int j = 0;
int answer = 0;
for(int i=mid;i<length;i++){
while(pos.get(j)<=startPos&&2*(pos.get(i)-startPos)+(startPos-pos.get(j))>k) j++;
if(pos.get(j)>startPos){
if(pos.get(i)-startPos<=k)
answer = Math.max(answer,sum[i]-(mid==0?0:sum[mid-1]));
}else if(Math.max(0,2*(pos.get(i)-startPos))+(startPos-pos.get(j))<=k) {
answer = Math.max(answer,sum[i]-(j==0?0:sum[j-1]));
}
}
mid = lowerBound(pos,startPos);
if(pos.get(mid)>startPos) mid--;
j = length-1;
for(int i=mid;i>=0;i--){
while(pos.get(j)>=startPos&&2*(startPos-pos.get(i))+(pos.get(j)-startPos)>k) j--;
if(pos.get(j)<startPos){
if(startPos-pos.get(i)<=k) {
answer = Math.max(answer,sum[mid]-(i==0?0:sum[i-1]));
}
}else if(2*(startPos-pos.get(i))+(pos.get(j)-startPos)<=k){
answer = Math.max(answer,sum[j]-(i==0?0:sum[i-1]));
}
}
return answer;
}
}
|
 image.png
image.png
本文标题:leetcode2106.摘水果
文章作者:meteor
发布时间:2023-05-04
最后更新:2023-05-04
原始链接:http://blog.zsenhe.com/2023/05/04/leetcode2106.%E6%91%98%E6%B0%B4%E6%9E%9C/
版权声明:本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 CN 许可协议。转载请注明出处!