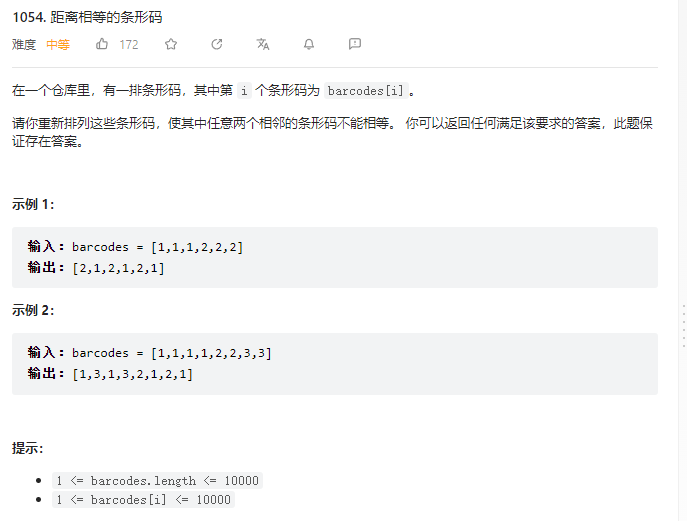
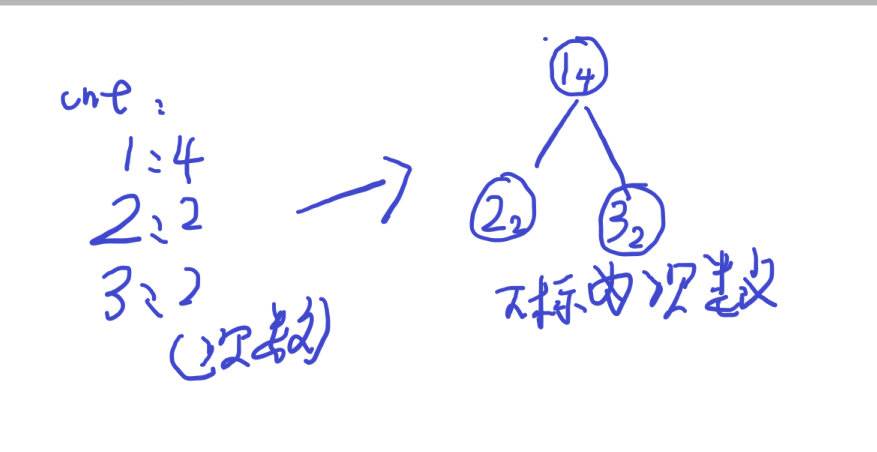
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| public static void down(Map<Integer,Integer> cnt,int size,int[] h,int u){
int t = u;
if(2*u<=size&&cnt.get(h[2*u])>cnt.get(h[u])) t = 2*u;
if((2*u+1)<=size&&cnt.get(h[2*u+1])>cnt.get(h[u])) t = 2*u+1;
if(t!=u) {
int tmp = h[u];
h[u] = h[t];
h[t] = tmp;
down(cnt, size, h, t);
}
}
public static int[] rearrangeBarcodes(int[] barcodes) {
Map<Integer,Integer> cnt = new HashMap<>();
for (int barcode : barcodes) {
cnt.put(barcode,cnt.getOrDefault(barcode,0)+1);
}
int[] heap = new int[cnt.size()+1];
int size = 0;
for (Integer integer : cnt.keySet()) {
heap[++size] = integer;
}
for(int i = size/2; i!=0 ; i--){
down(cnt,size,heap,i);
}
int last = -100;
int[] answer = new int[barcodes.length];
for(int i=0;i<barcodes.length;i++){
int idx = 1;
int top = heap[1];
if(top==last) {
if (size >= 3) {
if (cnt.get(heap[2]) > cnt.get(heap[3])) top = heap[idx = 2];
else top = heap[idx = 3];
} else top = heap[idx = 2];
}
answer[i] = last = top;
cnt.put(top,cnt.get(top)-1);
down(cnt,size,heap,idx);
}
return answer;
}
|